Advertisements
Advertisements
प्रश्न
A circular loop of radius r carries a current i. How should a long, straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
उत्तर
Given:
Magnitude of current = i
Radius of the loop = r
Magnetic field due to the loop at its centre,
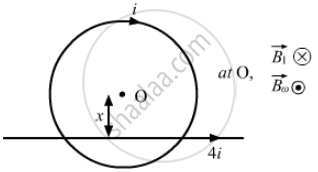
\[ \Rightarrow \frac{\mu_0 i}{2r} = \frac{\mu_0 4i}{2\pi x}\]
\[ \Rightarrow x = \frac{8r}{2\pi} = \frac{4r}{\pi}\]
This means that the wire is placed \[\frac{4r}{\pi}\] from the centre of the loop (as shown in the figure).
APPEARS IN
संबंधित प्रश्न
Using Biot-Savart law, deduce the expression for the magnetic field at a point (x) on the axis of a circular current carrying loop of radius R. How is the direction of the magnetic field determined at this point?
Use Biot-Savart's law to find the expression for the magnetic field due to a circular loop of radius 'r' carrying current 'I', at its centre ?
Derive the expression for the torque on a rectangular current carrying loop suspended in a uniform magnetic field.
Figure shows a long wire bent at the middle to form a right angle. Show that the magnitudes of the magnetic fields at the point P, Q, R and S are equal and find this magnitude.
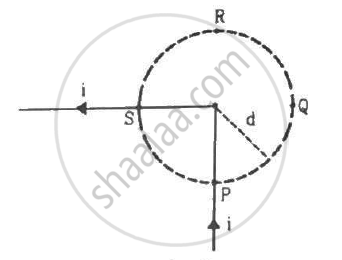
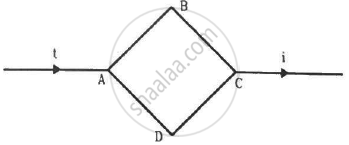
Figure shows a square loop ABCD with edge-length a. The resistance of the wire ABC is r and that of ADC is 2r. Find the magnetic field B at the centre of the loop assuming uniform wires.
Two circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes as well as the centres coincide. Find the magnitude of the magnetic field B at the common centre of the coils if the currents in the coils are (a) in the same sense (b) in the opposite sense.
A circular loop of radius 20 cm carries a current of 10 A. An electron crosses the plane of the loop with a speed of 2.0 × 106 m s−1. The direction of motion makes an angle of 30° with the axis of the circle and passes through its centre. Find the magnitude of the magnetic force on the electron at the instant it crosses the plane.
A circular loop of radius R carries a current I. Another circular loop of radius r(<<R) carries a current i and is placed at the centre of the larger loop. The planes of the two circles are at right angle to each other. Find the torque acting on the smaller loop.
Find the magnetic field B due to a semicircular wire of radius 10.0 cm carrying a current of 5.0 A at its centre of curvature.
A circular coil of 200 turns has a radius of 10 cm and carries a current of 2.0 A. (a) Find the magnitude of the magnetic field \[\vec{B}\] at the centre of the coil. (b) At what distance from the centre along the axis of the coil will the field B drop to half its value at the centre?
A circular loop of radius 4.0 cm is placed in a horizontal plane and carries an electric current of 5.0 A in the clockwise direction as seen from above. Find the magnetic field (a) at a point 3.0 cm above the centre of the loop (b) at a point 3.0 cm below the centre of the loop.
If we double the radius of a coil keeping the current through it unchanged, then the magnetic field at any point at a large distance from the centre becomes approximately.
A charged particle moving in a uniform magnetic field and losses 4% of its kinetic energy. The radius of curvature of its path changes by ______.
A small square loop of wire of side l is placed inside a large square loop of side L (L >> l). The loop is coplanar and their centers coincide. The mutual inductance of the system is proportional to is
The fractional change in the magnetic field intensity at a distance 'r' from centre on the axis of the current-carrying coil of radius 'a' to the magnetic field intensity at the centre of the same coil is ______.
(Take r < a).
Two horizontal thin long parallel wires, separated by a distance r carry current I each in the opposite directions. The net magnetic field at a point midway between them will be ______.
