Advertisements
Advertisements
प्रश्न
Two horizontal thin long parallel wires, separated by a distance r carry current I each in the opposite directions. The net magnetic field at a point midway between them will be ______.
विकल्प
zero
`((mu_0I)/(2pir))` vertically downward
`((2mu_0I)/r)` vertically upward
`((mu_0I)/(pir))` vertically downward
उत्तर
Two horizontal thin long parallel wires, separated by a distance r carry current I each in the opposite directions. The net magnetic field at a point midway between them will be zero.
Explanation:
When the right-hand thumb points in the direction of the current-carrying conductor, the fingers curl in the direction of the magnetic field around the current-carrying conductor, according to the thumb rule. As a result, the magnetic field at the spot caused by the wire on the left is pointing downwards. Using the same idea, the magnetic field at the place due to the right-hand side wire exists downwards. As a result, after adding the two magnetic fields, the net field is zero.
APPEARS IN
संबंधित प्रश्न
Use Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R.
Draw the magnetic field lines due to a circular wire carrying current I.
At a place, the horizontal component of earth's magnetic field is B and angle of dip is 60°. What is the value of horizontal component of the earth's magnetic field at equator?
Using Biot-Savart law, deduce the expression for the magnetic field at a point (x) on the axis of a circular current carrying loop of radius R. How is the direction of the magnetic field determined at this point?
A circular loop is kept in that vertical plane which contains the north-south direction. It carries a current that is towards north at the topmost point. Let A be a point on the axis of the circle to the east of it and B a point on this axis to the west of it. The magnetic field due to the loop
Figure shows a long wire bent at the middle to form a right angle. Show that the magnitudes of the magnetic fields at the point P, Q, R and S are equal and find this magnitude.
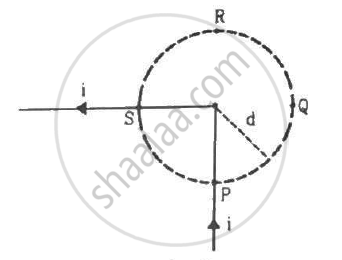
A circular loop of radius R carries a current I. Another circular loop of radius r(<<R) carries a current i and is placed at the centre of the larger loop. The planes of the two circles are at right angle to each other. Find the torque acting on the smaller loop.
A circular loop of radius r carrying a current i is held at the centre of another circular loop of radius R(>>r) carrying a current I. The plane of the smaller loop makes an angle of 30° with that of the larger loop. If the smaller loop is held fixed in this position by applying a single force at a point on its periphery, what would be the minimum magnitude of this force?
The magnitude of the magnetic field due to a circular coil of radius R carrying a current I at an axial distance x from the centre is ______.
The magnetic field at a distance r from a long wire carrying current I is 0.4 tesla. The magnetic field at a distance 2 r is ______.
The fractional change in the magnetic field intensity at a distance 'r' from centre on the axis of the current-carrying coil of radius 'a' to the magnetic field intensity at the centre of the same coil is ______.
(Take r < a).
