Advertisements
Advertisements
प्रश्न
A piece of wire carrying a current of 6.00 A is bent in the form of a circular are of radius 10.0 cm, and it subtends an angle of 120° at the centre. Find the magnetic field B due to this piece of wire at the centre.
उत्तर
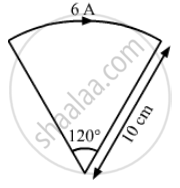
Given:
Magnitude of current, I = 6 A
Radius of the semi-circular wire, r = 10 cm
Angle subtended at the centre, θ = 120° = \[\frac{2\pi}{3}\]
∴ Required magnetic field at the centre of curvature
\[B = \frac{\mu_0 i}{2r}\frac{\theta}{2\pi}\]
\[ = \frac{4 \times {10}^{- 7} \times 5}{2 \times 10 \times {10}^{- 2}} \times \frac{2\pi}{3 \times 2\pi}\]
\[ = 4\pi \times {10}^{- 6} \]
\[ = 1 . 26 \times {10}^{- 5} T\]
APPEARS IN
संबंधित प्रश्न
Two concentric circular coils X and Y of radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A; coil Y has 25 turns and carries a current of 18 A. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.
At a place, the horizontal component of earth's magnetic field is B and angle of dip is 60°. What is the value of horizontal component of the earth's magnetic field at equator?
Using Biot-Savart law, deduce the expression for the magnetic field at a point (x) on the axis of a circular current carrying loop of radius R. How is the direction of the magnetic field determined at this point?
A steady electric current is flowing through a cylindrical conductor.
(a) The electric field at the axis of the conductor is zero.
(b) The magnetic field at the axis of the conductor is zero.
(c) The electric field in the vicinity of the conductor is zero.
(d) The magnetic field in the vicinity of the conductor is zero.
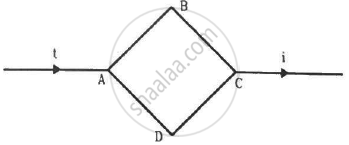
Figure shows a square loop ABCD with edge-length a. The resistance of the wire ABC is r and that of ADC is 2r. Find the magnetic field B at the centre of the loop assuming uniform wires.
Two circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes as well as the centres coincide. Find the magnitude of the magnetic field B at the common centre of the coils if the currents in the coils are (a) in the same sense (b) in the opposite sense.
Two circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes as well as the centres coincide. If the outer coil is rotated through 90° about a diameter, Find the magnitude of the magnetic field B at the common centre of the coils if the currents in the coils are (a) in the same sense (b) in the opposite sense.
A circular loop of radius R carries a current I. Another circular loop of radius r(<<R) carries a current i and is placed at the centre of the larger loop. The planes of the two circles are at right angle to each other. Find the torque acting on the smaller loop.
A circular loop of radius r carrying a current i is held at the centre of another circular loop of radius R(>>r) carrying a current I. The plane of the smaller loop makes an angle of 30° with that of the larger loop. If the smaller loop is held fixed in this position by applying a single force at a point on its periphery, what would be the minimum magnitude of this force?
Find the magnetic field B due to a semicircular wire of radius 10.0 cm carrying a current of 5.0 A at its centre of curvature.
A circular loop of radius r carries a current i. How should a long, straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
A circular coil of 200 turns has a radius of 10 cm and carries a current of 2.0 A. (a) Find the magnitude of the magnetic field \[\vec{B}\] at the centre of the coil. (b) At what distance from the centre along the axis of the coil will the field B drop to half its value at the centre?
A charge of 3.14 × 10−6 C is distributed uniformly over a circular ring of radius 20.0 cm. The ring rotates about its axis with an angular velocity of 60.0 rad s−1. Find the ratio of the electric field to the magnetic field at a point on the axis at a distance of 5.00 cm from the centre.
The magnitude of the magnetic field due to a circular coil of radius R carrying a current I at an axial distance x from the centre is ______.
A short bar magnet has a magnetic moment of 0. 65 J T-1, then the magnitude and direction of the magnetic field produced by the magnet at a distance 8 cm from the centre of magnet on the axis is ______.
Consider a circular current-carrying loop of radius R in the x-y plane with centre at origin. Consider the line intergral
`ℑ(L ) = |int_(-L)^L B.dl|` taken along z-axis.
- Show that ℑ(L) monotonically increases with L.
- Use an appropriate Amperian loop to show that ℑ(∞) = µ0I, where I is the current in the wire.
- Verify directly the above result.
- Suppose we replace the circular coil by a square coil of sides R carrying the same current I. What can you say about ℑ(L) and ℑ(∞)?
