Advertisements
Advertisements
प्रश्न
Using a graph paper, plot the point A (6, 4) and B (0, 4).
(a) Reflect A and B in the origin to get the image A’ and B’.
(b) Write the co-ordinates of A’ and B’.
(c) Sate the geometrical name for the figure ABA’B’.
(d) Find its perimeter.
उत्तर
(a)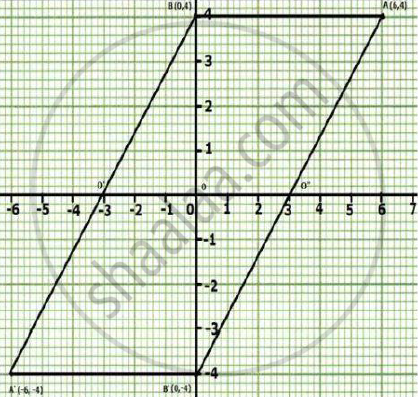
(b) Co-ordinates of A'=(-6,-4)
Co-ordinates of B'=(0,-4)
(c) ABA'B' is parallelogram.
(d) In ABA'B',BB'=8 units, A'B'=6 units
AB=A'B'=6units
∴ the perimeter of ABA'B'=AB+BA'+A'B'+B'A
=6+10+6+10
=32 units
APPEARS IN
संबंधित प्रश्न
Attempt this question on graph paper.
- Plot A (3, 2) and B (5, 4) on graph paper. Take 2 cm = 1 unit on both the axes.
- Reflect A and B in the x-axis to A’ and B’ respectively. Plot these points also on the same graph paper.
- Write down:
- the geometrical name of the figure ABB’A’;
- the measure of angle ABB’;
- the image of A” of A, when A is reflected in the origin.
- the single transformation that maps A’ to A”.
The points P (4, 1) and Q (–2, 4) are reflected in line y = 3. Find the co-ordinates of P’, the image of P and Q’, the image of Q.
A point P (–2, 3) is reflected in line x = 2 to point P’. Find the co-ordinates of P’.
A point P (a, b) is reflected in the x-axis to P’ (2, –3). Write down the values of a and b. P” is the image of P, reflected in the y-axis. Write down the co-ordinates of P”. Find the co-ordinates of P”’, when P is reflected in the line, parallel to y-axis, such that x = 4.
Points A and B have co-ordinates (3, 4) and (0, 2) respectively. Find the image:
- A’ of A under reflection in the x-axis.
- B’ of B under reflection in the line AA’.
- A” of A under reflection in the y-axis.
- B” of B under reflection in the line AA”.
The point P (5, 3) was reflected in the origin to get the image P’.
- Write down the co-ordinates of P’.
- If M is the foot of the perpendicular from P to the x-axis, find the co-ordinates of M.
- If N is the foot of the perpendicular from P’ to the x-axis, find the co-ordinates of N.
- Name the figure PMP’N.
- Find the area of the figure PMP’N.
The point P (3, 4) is reflected to P’ in the x-axis; and O’ is the image of O (the origin) when reflected in the line PP’. Write:
- the co-ordinates of P’ and O’.
- the length of the segments PP’ and OO’.
- the perimeter of the quadrilateral POP’O’.
- the geometrical name of the figure POP’O’.
- The point P (2, –4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.
- The point Q is reflected about the line y = 0 to get the image R. Find the co-ordinates of R.
- Name the figure PQR.
- Find the area of figure PQR.
Use a graph paper for this question.
(Take 2 cm = 1 unit on both x and y axes)
- Plot the following points: A(0, 4), B(2, 3), C(1, 1) and D(2, 0).
- Reflect points B, C, D on the y-axis and write down their coordinates. Name the images as B', C', D' respectively.
- Join the points A, B, C, D, D', C', B' and A in order, so as to form a closed figure. Write down the equation to the line about which if this closed figure obtained is folded, the two parts of the figure exactly coincide.
Points (3, 0) and (-1, 0) are invarient points under reflection in the line L1; point (0, -3) and (0, 1) are invarient points on reflection in line L2.
(i) Write the equation of the line L1 and L2.
(ii) Write down the images of points P(3, 4) and Q(-5, -2) on reflection in L1. Name the images as P' and Q' respectively.
(iii) Write down the images of P and Q on reflection in L2. Name the image as P'' and Q'' respectively.
