Advertisements
Advertisements
प्रश्न
Using Huygen's wave theory, show that (for refraction of light):
`sin i/sin r = "constant"`
where terms have their usual meaning. You must draw a neat and labelled diagram.
उत्तर
Let SS' represent the surface separating media 1 and 2 of refractive indices n1 and n2, respectively. Let c1 and c2 be the velocities of light in the two media. The second medium is optically denser than the first, hence c1 > c2.
APB is the incident wavefront. By the time the disturbance at B reaches C, the secondary wavelet from A has travelled a distance of AD = c2t, where t is the time it took the waves to travel the distance of BC. Therefore, BC= c1 t and AD= c2t.· With A as the centre and radius AD(= c2t), we draw a sphere and a tangent CD to the sphere is also drawn from the point C. Thus, CD represents the refracted plane wavefront. To prove that CD is the common wavefront, it is enough to show that in the time the disturbance travels from B to C or A to D, the disturbance at P reaches L. With M as the centre, we draw a sphere such that CD happens to be the tangent of the sphere.
From the similar triangles ACD and MCL,
`("AD")/("ML") = ("AC")/("MC")` ...(i)
Similarly, from similar triangles (ACE and MCN),
`("AE")/("MN") = ("AC")/("MC")` ...(ii)
From (i) and (ii),
`("AD")/("ML") = ("AE")/("MN")`
or `("AE")/("AD") = ("MN")/("ML")`
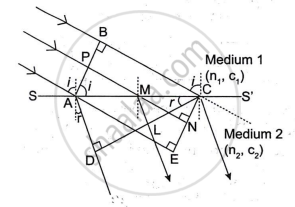
∵ AE = BC = c1t and AD = c2t, we can write,
`("AE")/("AD") = (c_1t)/(c_2t) = ("MN")/("ML")`
or `("BC")/("AD") = ("MN")/("ML") = (c_1)/(c_2)` ...(iii)
The radius of the secondary wavefront for point A is therefore AD, while the radius of the secondary wavefront for point M is ML.
Let r and i represent the angles of refraction and incidence, respectively.
From triangle ABC and ACD,
`sini/sinr = ("BC"/"AC")/("AD"/"AC") = ("BC")/("AD") = (c_1t)/(c_2t) = c_1/c_2 = ""_1n_2`
1n2 is constant and is called the refractive index of the second medium with respect to the first medium. So, `sini/sinr` = constant
APPEARS IN
संबंधित प्रश्न
Does the apparent depth of a tank of water change if viewed obliquely? If so, does the apparent depth increase or decrease?
The refractive index of diamond is much greater than that of ordinary glass. Is this fact of some use to a diamond cutter?
Monochromatic light of wavelength 589 nm is incident from air on a water surface. If µ for water is 1.33, find the wavelength, frequency and speed of the refracted light.
For the same value of angle of incidence, the angles of refraction in three media A, B and C are 15°, 25° and 35° respectively. In which medium would the velocity of light be minimum?
A laser light is focussed by a converging lens. Will there be a significant chromatic aberration?
What is mirage?
What is looming?
A ray of unpolarised light is incident on the surface of glass plate of µ = 1.54 at polarising angle, then angle of refraction is
Three immiscible liquids of densities d1 > d2 > d3 and refractive indices µ1 > µ2 > µ3 are put in a beaker. The height of each liquid column is `h/3`. A dot is made at the bottom of the beaker. For near normal vision, find the apparent depth of the dot.
A beam of light travels from air into a medium. Its speed and wavelength in the medium are 1.5 × 108 ms-1 and 230 nm respectively. The wavelength of light in the air will be ______.
