Advertisements
Advertisements
प्रश्न
Three immiscible liquids of densities d1 > d2 > d3 and refractive indices µ1 > µ2 > µ3 are put in a beaker. The height of each liquid column is `h/3`. A dot is made at the bottom of the beaker. For near normal vision, find the apparent depth of the dot.
उत्तर
Coordinate convention: At the first surface (+ upward and – ve downward)
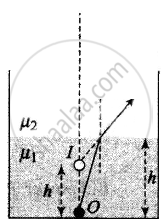
`mu_2/h^' - mu_1/(-h) = (mu_2 - mu_1)/(oo)` (infinity because the surface is plane),
or `h^' = mu_2/mu_1 h`.
The negative sign shows that it is on the side of the object
`h^'` is the apparent depth of O after refraction from the interface.

The position of image of O after refraction from surface-1. If seen from `mu_2`, the apparent depth is `h_1`
`h_1 = mu_2/mu_1 h/3`
The negative sign shows that it is on the side of the object.
Since the image formed by surface-1 will act as an object for surface-3. If seen from `mu_3`, the apparent depth is `h_2`.
Similarly, the image formed by Medium 2, O2 acts as an object for MEdium 3.
`h_2 = mu_3/mu_2 (mu_2/mu_1 h/3 + h/3) = - h/3(mu_3/mu_2 + mu_2/mu_1)`
Finally, the image formed by surface-2 will act as an object for surface-2. If seen from the outside, the apparent depth is `h_3`.
`h_3 = - 1/mu_3 [h/3 + h/3(mu_3/mu_2 + mu_3/mu_1)] = - h/3 (1/mu_1 + 1/mu_2 + 1/mu_3)`
Hence apparent depth of dot is `h/3(1/mu_1 + 1/mu_2 + 1/mu_3)`
Xa is apparent depth.
APPEARS IN
संबंधित प्रश्न
Does the apparent depth of a tank of water change if viewed obliquely? If so, does the apparent depth increase or decrease?
The refractive index of diamond is much greater than that of ordinary glass. Is this fact of some use to a diamond cutter?
Is the formula "Real depth/Apparent depth = μ" valid if viewed from a position quite away from the normal?
If the light moving in a straight line bends by a small but fixed angle, it may be a case of
(a) reflection
(b) refraction
(c) diffraction
(d) dispersion.
Consider the situation in figure. The bottom of the pot is a reflecting plane mirror, S is a small fish and T is a human eye. Refractive index of water is μ. (a) At what distance(s) from itself will the fish see the image(s) of the eye? (b) At what distance(s) from itself will the eye see the image(s) of the fish.

Figure shows a transparent hemisphere of radius 3.0 cm made of a material of refractive index 2.0. (a) A narrow beam of parallel rays is incident on the hemisphere as shown in the figure. Are the rays totally reflected at the plane surface? (b) Find the image formed by the refraction at the first surface. (c) Find the image formed by the reflection or by the refraction at the plane surface. (d) Trace qualitatively the final rays as they come out of the hemisphere.

Obtain the equation for critical angle.
What is looming?
A light travels through water in the beaker. The height of water column is 'h'. Refractive index of water is 'μw'. If c is velocity of light in air, the time taken by light to travel through water will ______.
For a rectangular slab, refraction takes place at ______.
