Advertisements
Advertisements
Question
Three immiscible liquids of densities d1 > d2 > d3 and refractive indices µ1 > µ2 > µ3 are put in a beaker. The height of each liquid column is `h/3`. A dot is made at the bottom of the beaker. For near normal vision, find the apparent depth of the dot.
Solution
Coordinate convention: At the first surface (+ upward and – ve downward)
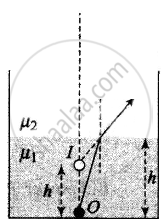
`mu_2/h^' - mu_1/(-h) = (mu_2 - mu_1)/(oo)` (infinity because the surface is plane),
or `h^' = mu_2/mu_1 h`.
The negative sign shows that it is on the side of the object
`h^'` is the apparent depth of O after refraction from the interface.

The position of image of O after refraction from surface-1. If seen from `mu_2`, the apparent depth is `h_1`
`h_1 = mu_2/mu_1 h/3`
The negative sign shows that it is on the side of the object.
Since the image formed by surface-1 will act as an object for surface-3. If seen from `mu_3`, the apparent depth is `h_2`.
Similarly, the image formed by Medium 2, O2 acts as an object for MEdium 3.
`h_2 = mu_3/mu_2 (mu_2/mu_1 h/3 + h/3) = - h/3(mu_3/mu_2 + mu_2/mu_1)`
Finally, the image formed by surface-2 will act as an object for surface-2. If seen from the outside, the apparent depth is `h_3`.
`h_3 = - 1/mu_3 [h/3 + h/3(mu_3/mu_2 + mu_3/mu_1)] = - h/3 (1/mu_1 + 1/mu_2 + 1/mu_3)`
Hence apparent depth of dot is `h/3(1/mu_1 + 1/mu_2 + 1/mu_3)`
Xa is apparent depth.
APPEARS IN
RELATED QUESTIONS
Light of wavelength 5000 Å propagating in air gets partly reflected from the surface of water. How will the wavelengths and frequencies of the reflected and refracted light be affected?
Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length is to be 20 cm?
A small pin fixed on a table top is viewed from above from a distance of 50 cm. By what distance would the pin appear to be raised if it is viewed from the same point through a 15 cm thick glass slab held parallel to the table? Refractive index of glass = 1.5. Does the answer depend on the location of the slab?
A point object is placed at a distance of 30 cm from a convex mirror of focal length 30 cm. The image will form at
If the light moving in a straight line bends by a small but fixed angle, it may be a case of
(a) reflection
(b) refraction
(c) diffraction
(d) dispersion.
A point ‘O’ marked on the surface of a glass sphere of diameter 20 cm is viewed through glass from the position directly opposite to the point O. If the refractive index of the glass is 1.5, find the position of the image formed. Also, draw the ray diagram for the formation of the image.
Choose the correct option.
There are different fish, monkeys, and water of the habitable planet of the star Proxima b. A fish swimming underwater feels that there is a monkey at 2.5 m on the top of a tree. The same monkey feels that the fish is 1.6 m below the water surface. Interestingly, height of the tree and the depth at which the fish is swimming are exactly same. Refractive index of that water must be
A light travels through water in the beaker. The height of water column is 'h'. Refractive index of water is 'μw'. If c is velocity of light in air, the time taken by light to travel through water will ______.
Light travels from an optically denser medium 'A' into the optically rarer medium 'B' with speeds 1.8 × 108 m/s and 2.7 × 108 m/s respectively. Then critical angle between them is ______.
(µ1 and µ2 are the refractive indices of media A and B respectively.)
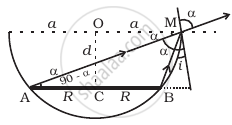
A circular disc of radius ‘R’ is placed co-axially and horizontally inside an opaque hemispherical bowl of radius ‘a’ (Figure). The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index µ and the near edge of the disc becomes just visible. How far below the top of the bowl is the disc placed?