Advertisements
Advertisements
Question
Choose the correct option.
There are different fish, monkeys, and water of the habitable planet of the star Proxima b. A fish swimming underwater feels that there is a monkey at 2.5 m on the top of a tree. The same monkey feels that the fish is 1.6 m below the water surface. Interestingly, height of the tree and the depth at which the fish is swimming are exactly same. Refractive index of that water must be
Options
`6/5`
`5/4`
`4/3`
`7/5`
Solution
`5/4`
Explanation:
As, height of the tree = depth at which fish swimming, Real depth, or height in both conditions is same, (say) x.
∴ For monkey, as apparent depth = 1.6 m,
`"n"_"water"/"n"_"air"="Real depth"/"Apparent depth"="x"/1.6`
For fish, as apparent height = 2.5 m,
`"n"_"air"/"n"_"water"="Real height"/"Apparent height"="x"/2.5`
∴ `"x"/1.6xx"x"/2.5` = 1
∴ x2 = 4 ⇒ x = 2
∴ `"n"_"water"/"n"_"air"="x"/1.6=2/1.6=5/4`
APPEARS IN
RELATED QUESTIONS
Figures (a) and (b) show the refraction of a ray in air incident at 60° with the normal to a glass-air and water-air interface, respectively. Predict the angle of refraction in the glass when the angle of incidence in water is 45° with the normal to a water-glass interface [Figure (c)].
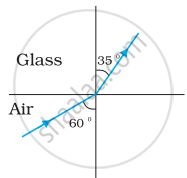 |
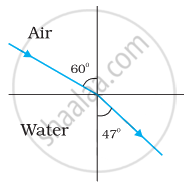 |
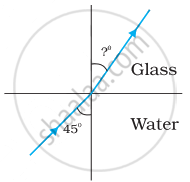 |
| (a) | (b) | (c) |
Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length is to be 20 cm?
- Figure shows a cross-section of a ‘light pipe’ made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure?
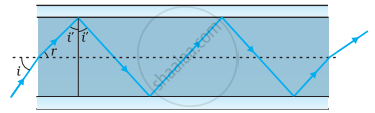
- What is the answer if there is no outer covering of the pipe?
Does the apparent depth of a tank of water change if viewed obliquely? If so, does the apparent depth increase or decrease?
A converging lens has a focal length of 20 cm in air. It is made of a material of refractive index 1·6. If it is immersed in a liquid of refractive index 1·3, find its new focal length.
Determine the value of the angle of incidence for a ray of light travelling from a medium of refractive index \[\mu_1 = \sqrt{2}\] into the medium of refractive index \[\mu_2 = 1\] so that it just grazes along the surface of separation.
A narrow beam of white light goes through a slab having parallel faces.
(a) The light never splits in different colours
(b) The emergent beam is white
(c) The light inside the slab is split into different colours
(d) The light inside the slab is white
Consider the situation in figure. The bottom of the pot is a reflecting plane mirror, S is a small fish and T is a human eye. Refractive index of water is μ. (a) At what distance(s) from itself will the fish see the image(s) of the eye? (b) At what distance(s) from itself will the eye see the image(s) of the fish.

A point ‘O’ marked on the surface of a glass sphere of diameter 20 cm is viewed through glass from the position directly opposite to the point O. If the refractive index of the glass is 1.5, find the position of the image formed. Also, draw the ray diagram for the formation of the image.
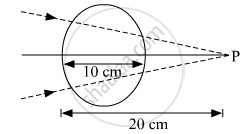
A converging beam of light traveling in air converges at a point P as shown in the figure. When a glass sphere of refractive index 1⋅5 is introduced in between the path of the beam, calculate the new position of, the image. Also, draw the ray diagram for the image formed.
Answer the following question.
Define absolute refractive index and relative refractive index. Explain in brief with an illustration for each.
What is optical path? Obtain the equation for optical path of a medium of thickness d and refractive index n.
What is angle of deviation due to refraction?
What is relative refractive index?
Obtain the equation for critical angle.
What is Snell’s window?
Write a note on optical fibre.
Obtain the equation for radius of illumination (or) Snell’s window.
A light travels through water in the beaker. The height of water column is 'h'. Refractive index of water is 'μw'. If c is velocity of light in air, the time taken by light to travel through water will ______.
The critical angle is maximum when light travels from ______.
`(a^mu"w"=4/3,a^mug=3/2)`
A concave mirror of focal length 'f1' is placed at a distance 'd' from a convex lens of focal length 'f2'. A parallel beam of light coming from infinity parallel to principal axis falls on the convex lens and then after refraction falls on the concave mirror. If it is to retrace the path, the distance 'd' should be ______.
If `"^imu_j` represents refractive index, when a light ray goes from medium i to medium j, then the product `"^2mu_1 xx ^3mu_2 xx ^4mu_3` is equal to ______.
For a rectangular slab, refraction takes place at ______.
Consider an extended object immersed in water contained in a plane trough. When seen from close to the edge of the trough the object looks distorted because ______.
- the apparent depth of the points close to the edge are nearer the surface of the water compared to the points away from the edge.
- the angle subtended by the image of the object at the eye is smaller than the actual angle subtended by the object in air.
- some of the points of the object far away from the edge may not be visible because of total internal reflection.
- water in a trough acts as a lens and magnifies the object.
Three immiscible liquids of densities d1 > d2 > d3 and refractive indices µ1 > µ2 > µ3 are put in a beaker. The height of each liquid column is `h/3`. A dot is made at the bottom of the beaker. For near normal vision, find the apparent depth of the dot.
A convex lens made of material of refractive index 1.5 and having a focal length of 10 cm is immersed in a liquid of refractive index 3.0. The lens will behave as ______.
Using Huygen's wave theory, show that (for refraction of light):
`sin i/sin r = "constant"`
where terms have their usual meaning. You must draw a neat and labelled diagram.
