Advertisements
Advertisements
Question
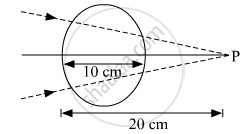
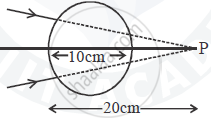
A converging beam of light traveling in air converges at a point P as shown in the figure. When a glass sphere of refractive index 1⋅5 is introduced in between the path of the beam, calculate the new position of, the image. Also, draw the ray diagram for the image formed.
Solution
For refraction at curved surfaces, using the relation, `mu_2/"v" - mu_1/"u" = (mu_2 - mu_1)/"R"` .......(1)
For the given conditions:
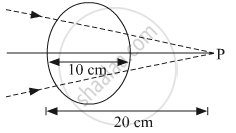
The first refraction takes place at the left side of the sphere. As the incident rays are going to converge at a point 20 cm away from the pole of the curved surface so,
`mu = +20 "cm", "R" =+5 "cm", mu_1 = 1, mu_2 = 1.5`
Using equation 1,
`1.5/"v" - 1/20 = (1.5 - 1)/5`
⇒ `1.5/"v" = 0.5/5 + 1/20 = 1/10 + 1/20 = 3/20`
⇒ v = 10 cm
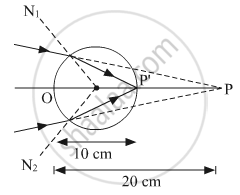
As the image distance equal to the diameter of the glass sphere, hence the final image will form at point Q, on the circumference of the sphere, as shown in the figure.
APPEARS IN
RELATED QUESTIONS
Monochromatic light of wavelength 589 nm is incident from air on a water surface. If µ for water is 1.33, find the wavelength, frequency and speed of the refracted light.
A glass lens of refractive index 1.45 disappears when immersed in a liquid. What is the value of refractive index of the liquid?
Why does a diamond shine more than a glass piece cut to the same shape?
A converging beam of light travelling in air converges at a point P as shown in the figure. When a glass sphere of refractive index 1 . 5 is introduced in between the path of the beam, calculate the new position of the image. Also draw the ray diagram for the image formed.
Answer the following question.
Define absolute refractive index and relative refractive index. Explain in brief with an illustration for each.
What is optical path? Obtain the equation for optical path of a medium of thickness d and refractive index n.
What is angle of deviation due to refraction?
What is looming?
Three immiscible liquids of densities d1 > d2 > d3 and refractive indices µ1 > µ2 > µ3 are put in a beaker. The height of each liquid column is `h/3`. A dot is made at the bottom of the beaker. For near normal vision, find the apparent depth of the dot.
A circular disc of radius ‘R’ is placed co-axially and horizontally inside an opaque hemispherical bowl of radius ‘a’ (Figure). The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index µ and the near edge of the disc becomes just visible. How far below the top of the bowl is the disc placed?