Advertisements
Advertisements
Question
A converging lens has a focal length of 20 cm in air. It is made of a material of refractive index 1·6. If it is immersed in a liquid of refractive index 1·3, find its new focal length.
Solution
\[\text { Case I: Lens in air }\]
\[\text { Let the focal length of lens in air be F}_{air} \]
\[\text { Given that } \]
\[ F_{air} = 20 cm \]
\[ n_1 = 1 (air)\]
\[ n_2 = 1 . 6\]
\[\text { According to lens maker's formula }: \]
\[\frac{1}{F_{air}} = [\frac{n_2}{n_1} - 1][\frac{1}{R_1} - \frac{1}{R_2}]\]
\[\frac{1}{20} = [\frac{1 . 6}{1} - 1][\frac{1}{R_1} - \frac{1}{R_2}]\]
\[\frac{1}{20} = [0 . 6][\frac{1}{R_1} - \frac{1}{R_2}] . . . . . . (i)\]
\[\text { Case II: Lens in liquid }\]
\[\text { Let the focal length of lens in liquid be F}_{liquid} \]
\[\text { Given that } \]
\[ n_1 = 1 . 3 \text { (liquid) }\]
\[ n_2 = 1 . 6\]
\[\text { According to lens maker's formula }: \]
\[\frac{1}{F_{liquid}} = [\frac{1 . 6}{1 . 3} - 1][\frac{1}{R_1} - \frac{1}{R_2}]\]
\[\frac{1}{F_{liquid}} = [0 . 2307][\frac{1}{R_1} - \frac{1}{R_2}] . . . . . . (ii)\]
\[\text { Dividing (i) by (ii), we get}\]
\[\frac{F_{liquid}}{20} = \frac{0 . 6}{0 . 2307}\]
\[ F_{liquid} = 52 . 0156 cm\]
APPEARS IN
RELATED QUESTIONS
Figures (a) and (b) show the refraction of a ray in air incident at 60° with the normal to a glass-air and water-air interface, respectively. Predict the angle of refraction in the glass when the angle of incidence in water is 45° with the normal to a water-glass interface [Figure (c)].
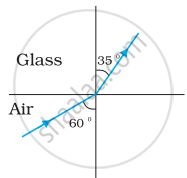 |
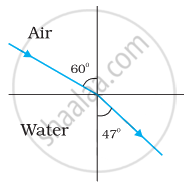 |
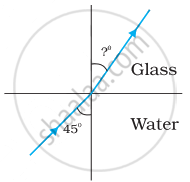 |
| (a) | (b) | (c) |
- Figure shows a cross-section of a ‘light pipe’ made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure?
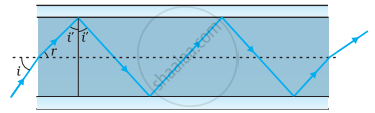
- What is the answer if there is no outer covering of the pipe?
A glass lens of refractive index 1.45 disappears when immersed in a liquid. What is the value of refractive index of the liquid?
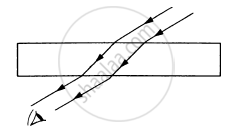
A narrow beam of light passes through a slab obliquely and is then received by an eye following figure. The index of refraction of the material in the slab fluctuates slowly with time. How will it appear to the eye? The twinkling of stars has a similar explanation.
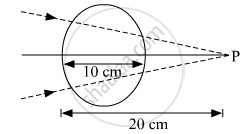
A converging beam of light traveling in air converges at a point P as shown in the figure. When a glass sphere of refractive index 1⋅5 is introduced in between the path of the beam, calculate the new position of, the image. Also, draw the ray diagram for the image formed.
What is angle of deviation due to refraction?
Obtain the equation for apparent depth.
Explain the reason for glittering of diamond.
A ray of unpolarised light is incident on the surface of glass plate of µ = 1.54 at polarising angle, then angle of refraction is
Three immiscible liquids of densities d1 > d2 > d3 and refractive indices µ1 > µ2 > µ3 are put in a beaker. The height of each liquid column is `h/3`. A dot is made at the bottom of the beaker. For near normal vision, find the apparent depth of the dot.
