Advertisements
Advertisements
Question
- Figure shows a cross-section of a ‘light pipe’ made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure?
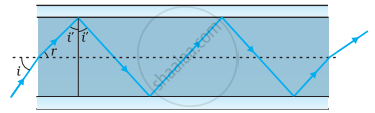
- What is the answer if there is no outer covering of the pipe?
Solution
(a) Refractive index of the glass fibre, μ1 = 1.68
Refractive index of the outer covering of the pipe, μ2 = 1.44
Angle of incidence = i
Angle of refraction = r
Angle of incidence at the interface = i'
The refractive index (μ) of the inner core − outer core interface is given as:
`μ = μ_2/μ_1 = 1/(sin "i'")`
`sin "i'" = (μ_1)/(μ_2)`
= `1.44/1.68`
= 0.8571
∴ i' = 59°
For the critical angle, total internal reflection (TIR) takes place only when i > i', i.e., i > 59°
Maximum angle of reflection, rmax = 90° − i' = 90° − 59° = 31°
Let, imax be the maximum angle of incidence.
The refractive index at the air-glass interface, μ1 = 1.68
We have the relation for the maximum angles of incidence and reflection as:
`μ_1 = (sin "i"_"max")/sin "r"_"max"`
sin imax = μ1 sin rmax
= 1.68 sin 31°
= 1.68 × 0.5150
= 0.8652
∴ imax = sin−1 0.8652 ≈ 60°
Thus, all the rays incident at angles lying in the range 0 < i < 60° will suffer total internal reflection
(b) If the outer covering of the pipe is not present, then:
Refractive index of the outer pipe, μ1 = Refractive index of air = 1
For the angle of incidence i = 90°, we can write Snell’s law at the air − pipe interface as:
`sin "i"/sin "r" = μ_2` = 1.68
`sin "r" = (sin 90°)/1.68 = 1/1.68`
`"r" = sin^(-1) (0.5952)`
= 36.5°
∴ i' = 90° − 36.5° = 53.5°
Since i' > r, all incident rays will suffer total internal reflection.
APPEARS IN
RELATED QUESTIONS
Why does a diamond shine more than a glass piece cut to the same shape?
A point object is placed at a distance of 30 cm from a convex mirror of focal length 30 cm. The image will form at
If the light moving in a straight line bends by a small but fixed angle, it may be a case of
(a) reflection
(b) refraction
(c) diffraction
(d) dispersion.
A vessel contains water up to a height of 20 cm and above it an oil up to another 20 cm. The refractive indices of the water and the oil are 1.33 and 1.30 respectively. Find the apparent depth of the vessel when viewed from above.
Answer the following question.
Define absolute refractive index and relative refractive index. Explain in brief with an illustration for each.
What is a principle of reversibility?
What is critical angle and total internal reflection?
Explain the reason for glittering of diamond.
What is mirage?
Write a short note on the prisms making use of total internal reflection.
How does an endoscope work?
Derive the equation for acceptance angle and numerical aperture, of optical fiber.
Obtain the equation for lateral displacement of light passing through a glass slab.
The critical angle is maximum when light travels from ______.
`(a^mu"w"=4/3,a^mug=3/2)`
When a ray of light is incident normally on one refracting surface of an equilateral prism of refractive index 1.5, the emerging ray ______.
`[sin^-1(1/1.5)=41.8^circ]`
The optical density of turpentine is higher than that of water while its mass density is lower. Figure shows a layer of turpentine floating over water in a container. For which one of the four rays incident on turpentine in figure, the path shown is correct?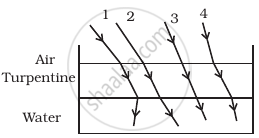
A convex lens made of material of refractive index 1.5 and having a focal length of 10 cm is immersed in a liquid of refractive index 3.0. The lens will behave as ______.
