Advertisements
Advertisements
Question
Derive the equation for acceptance angle and numerical aperture, of optical fiber.
Solution
- To ensure the critical angle incident in the core-cladding boundary inside the optical fibre, the light should be incident at a certain angle at the end of the optical fiber while entering into it. This angle is called an acceptance angle.
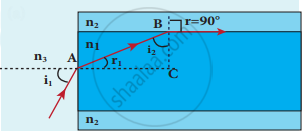
acceptance angle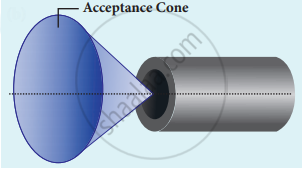
acceptance cone - By Snell’s law
n3 sin ia = n1 sin ra
To have the internal reflection inside optical fibre,
n1 sin i1 = n2 sin 90°
n1 sin ic = n2 sin 90° = 1
∴ sin ic = `"n"_2/"n"_1` - From the right angle triangle AABC,
ic = 90° – ra
Now, equation becomes
sin (90° – ra) = `"n"_2/"n"_1` - Using trigonometry,
cos ra = `"n"_2/"n"_1`
sin ra = `sqrt(1 - cos^2 "r"_"a")`
Substituting for cos ra
sin ra = `sqrt(1 - ("n"_2/"n"_1)^2) = sqrt(("n"_1^2 - "n"_2^2)/"n"_1^2)`
Substituting this in equation (1)
n3 sin ia = `"n"_1 sqrt(("n"_1^2 - "n"_2^2)/"n"_1^2) = sqrt("n"_1^2 - "n"_2^2)`
On further simplification,
sin ia = `sqrt(("n"_1^2 - "n"_2^2)/"n"_3)` or sin ia = `sqrt(("n"_1^2 - "n"_2^2)/"n"_3)`
`"i"_"a" = sin^-1 (sqrt(("n"_1^2 - "n"_2^2)/"n"_3))`
If outer medium is air, then n3 = 1. The acceptance angle ia becomes,
`"i"_"a" = sin^-1 (sqrt("n"_1^2 - "n"_2^2))` - Light can have any angle of incidence from o to ia with the normal at the end of the optical fibre forming a conical shape called acceptance cone.
The term (n3 sin ia) is called numerical aperture NA of the optical fibre
NA = n3 sin ia = `sqrt("n"_1^2 - "n"_2^2)` - 6. If outer medium is air, then n3 = 1. The numeric aperture NA becomes,
NA = sin ia = `sqrt("n"_1^2 - "n"_2^2)`
APPEARS IN
RELATED QUESTIONS
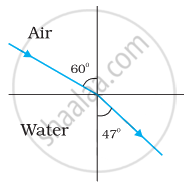
Figures (a) and (b) show the refraction of a ray in air incident at 60° with the normal to a glass-air and water-air interface, respectively. Predict the angle of refraction in the glass when the angle of incidence in water is 45° with the normal to a water-glass interface [Figure (c)].
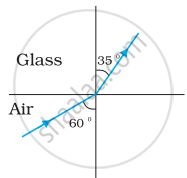 |
 |
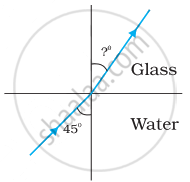 |
| (a) | (b) | (c) |
The refractive index of diamond is much greater than that of ordinary glass. Is this fact of some use to a diamond cutter?
What is looming?
How does an endoscope work?
A ray of light travels from air to water to glass and aga in from glass to air. Refractive index of water with respect to air is 'x' glass with respect to water is 'y' and air with respect to glass is 'z'. which one of the following is correct?
An object is immersed in a fluid of refractive index 'µ'. In order that the object becomes invisible when observed from outside, it should ______.
A ray of light passes through equilateral prism such that the angle of incidence is equal to angle of emergence and each of these angles is equal to `(3/4)^"th"` the angle of prism. The angle of deviation is ______.
Light travels in two media A and B with speeds 1.8 × 108 ms−1 and 2.4 × 108 ms−1 respectively. Then the critical angle between them is:
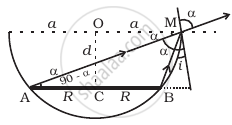
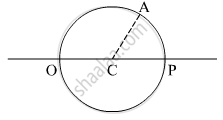
A circular disc of radius ‘R’ is placed co-axially and horizontally inside an opaque hemispherical bowl of radius ‘a’ (Figure). The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index µ and the near edge of the disc becomes just visible. How far below the top of the bowl is the disc placed?