Advertisements
Advertisements
प्रश्न
Derive the equation for acceptance angle and numerical aperture, of optical fiber.
उत्तर
- To ensure the critical angle incident in the core-cladding boundary inside the optical fibre, the light should be incident at a certain angle at the end of the optical fiber while entering into it. This angle is called an acceptance angle.
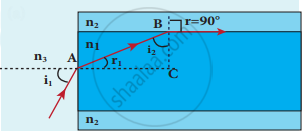
acceptance angle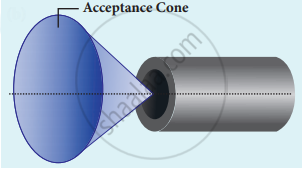
acceptance cone - By Snell’s law
n3 sin ia = n1 sin ra
To have the internal reflection inside optical fibre,
n1 sin i1 = n2 sin 90°
n1 sin ic = n2 sin 90° = 1
∴ sin ic = `"n"_2/"n"_1` - From the right angle triangle AABC,
ic = 90° – ra
Now, equation becomes
sin (90° – ra) = `"n"_2/"n"_1` - Using trigonometry,
cos ra = `"n"_2/"n"_1`
sin ra = `sqrt(1 - cos^2 "r"_"a")`
Substituting for cos ra
sin ra = `sqrt(1 - ("n"_2/"n"_1)^2) = sqrt(("n"_1^2 - "n"_2^2)/"n"_1^2)`
Substituting this in equation (1)
n3 sin ia = `"n"_1 sqrt(("n"_1^2 - "n"_2^2)/"n"_1^2) = sqrt("n"_1^2 - "n"_2^2)`
On further simplification,
sin ia = `sqrt(("n"_1^2 - "n"_2^2)/"n"_3)` or sin ia = `sqrt(("n"_1^2 - "n"_2^2)/"n"_3)`
`"i"_"a" = sin^-1 (sqrt(("n"_1^2 - "n"_2^2)/"n"_3))`
If outer medium is air, then n3 = 1. The acceptance angle ia becomes,
`"i"_"a" = sin^-1 (sqrt("n"_1^2 - "n"_2^2))` - Light can have any angle of incidence from o to ia with the normal at the end of the optical fibre forming a conical shape called acceptance cone.
The term (n3 sin ia) is called numerical aperture NA of the optical fibre
NA = n3 sin ia = `sqrt("n"_1^2 - "n"_2^2)` - 6. If outer medium is air, then n3 = 1. The numeric aperture NA becomes,
NA = sin ia = `sqrt("n"_1^2 - "n"_2^2)`
APPEARS IN
संबंधित प्रश्न
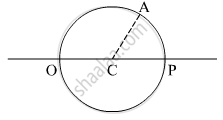
- Figure shows a cross-section of a ‘light pipe’ made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure?
- What is the answer if there is no outer covering of the pipe?
The refractive index of diamond is much greater than that of ordinary glass. Is this fact of some use to a diamond cutter?
Determine the value of the angle of incidence for a ray of light travelling from a medium of refractive index \[\mu_1 = \sqrt{2}\] into the medium of refractive index \[\mu_2 = 1\] so that it just grazes along the surface of separation.
Is the formula "Real depth/Apparent depth = μ" valid if viewed from a position quite away from the normal?
Write a note on optical fibre.
Light travels from an optically denser medium 'A' into the optically rarer medium 'B' with speeds 1.8 × 108 m/s and 2.7 × 108 m/s respectively. Then critical angle between them is ______.
(µ1 and µ2 are the refractive indices of media A and B respectively.)
Light travels in two media A and B with speeds 1.8 × 108 ms−1 and 2.4 × 108 ms−1 respectively. Then the critical angle between them is:
The optical density of turpentine is higher than that of water while its mass density is lower. Figure shows a layer of turpentine floating over water in a container. For which one of the four rays incident on turpentine in figure, the path shown is correct?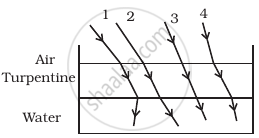
Show that for a material with refractive index `µ ≥ sqrt(2)`, light incident at any angle shall be guided along a length perpendicular to the incident face.
