Advertisements
Advertisements
प्रश्न
Obtain the equation for radius of illumination (or) Snell’s window.
उत्तर
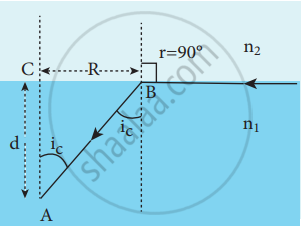
- When light entering the water from outside is seen from inside the water, the view is restricted to a particular angle equal to the critical angle ic.
- This restricted illuminated circular area is called Snell’s window.
- The angle of view for water animals is restricted to twice the critical angle 2ic. The critical angle for water is 48.6°. The angle of view is 97.2°.
- The radius R of the circular area depends on the depth d from which it is seen and the refractive indices of the media.
- Light is seen from a point A at a depth d.
Snell’s law
n1 sin ic = n2 sin 90°
n1 sin ic = n2 ∵ sin 90° = 1
sin ic = `"n"_2/"n"_1` - From the Right angle triangle ∆ ABC,
sin ic = `"CB"/"AB" = "R"/sqrt("d"^2 + "R"^2)`
Equating the above two equations
`"R"/sqrt("d"^2 + "R"^2) = ("n"_2/"n"_1)`
Radius of Snell’s window
Squaring on both sides,
`"R"^2/("R"^2 + "d"^2) = ("n"_2/"n"_1)^2`
Taking reciprocal,
`("R"^2 + "d"^2)/"R"^2 = ("n"_1/"n"_2)^2`
On further simplifying,
`1 + "d"^2/"R"^2 = ("n"_1/"n"_2)^2; "d"^2/"R"^2 = ("n"_1/"n"_2)^2 - 1;`
`"d"^2/"R"^2 = ("n"_1^2/"n"_2^2) - 1 = ("n"_1^2 - "n"_2^2)/"n"_2^2`
Again taken reciprocal and rearranging
`"R"^2/"R"^2 = "n"_2^2/("n"_1^2 - "n"_2^2); "R"^2 = "d"^2("n"_2^2/("n"_1^2 - "n"_2^2))`
Tha radius of illumination is,
R = d`sqrt(("n"_2^2)/("n"_1^2 - "n"_2^2))`
If the rarer medium outside in air, then, n2 = 1, and we can take n1 = n
R = d`1/sqrt("n"^2 - 1)` (or) R = `"d"/sqrt("n"^2 - 1)`
APPEARS IN
संबंधित प्रश्न
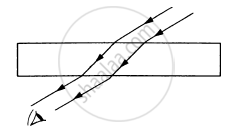
A narrow beam of light passes through a slab obliquely and is then received by an eye following figure. The index of refraction of the material in the slab fluctuates slowly with time. How will it appear to the eye? The twinkling of stars has a similar explanation.
A pole of length 1.00 m stands half dipped in a swimming pool with water level 50.0 cm higher than the bed. The refractive index of water is 1.33 and sunlight is coming at an angle of 45° with the vertical. Find the length of the shadow of the pole on the bed.
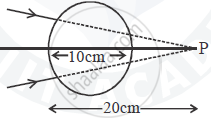
A converging beam of light travelling in air converges at a point P as shown in the figure. When a glass sphere of refractive index 1 . 5 is introduced in between the path of the beam, calculate the new position of the image. Also draw the ray diagram for the image formed.
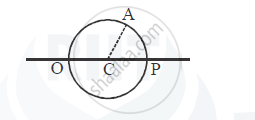
A point ‘O’ marked on the surface of a glass sphere of diameter 20 cm is viewed through glass from the position directly opposite to the point O. If the refractive index of the glass is 1.5, find the position of the image formed. Also, draw the ray diagram for the formation of the image.
Why do stars twinkle?
Obtain the equation for critical angle.
An object is immersed in a fluid of refractive index 'µ'. In order that the object becomes invisible when observed from outside, it should ______.
The critical angle for a ray of light from glass to air is 'θ' and refractive index of glass with respect to air is 'n'. If a ray of light is incident from air to glass at an angle 'θ', then corresponding angle of refraction is ______.
A circular disc of radius ‘R’ is placed co-axially and horizontally inside an opaque hemispherical bowl of radius ‘a’ (Figure). The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index µ and the near edge of the disc becomes just visible. How far below the top of the bowl is the disc placed?
Using Huygen's wave theory, show that (for refraction of light):
`sin i/sin r = "constant"`
where terms have their usual meaning. You must draw a neat and labelled diagram.
