Advertisements
Advertisements
प्रश्न
Obtain the equation for radius of illumination (or) Snell’s window.
उत्तर
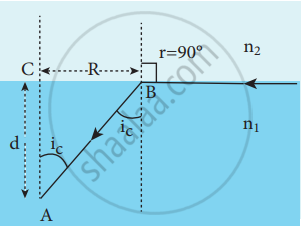
- When light entering the water from outside is seen from inside the water, the view is restricted to a particular angle equal to the critical angle ic.
- This restricted illuminated circular area is called Snell’s window.
- The angle of view for water animals is restricted to twice the critical angle 2ic. The critical angle for water is 48.6°. The angle of view is 97.2°.
- The radius R of the circular area depends on the depth d from which it is seen and the refractive indices of the media.
- Light is seen from a point A at a depth d.
Snell’s law
n1 sin ic = n2 sin 90°
n1 sin ic = n2 ∵ sin 90° = 1
sin ic = `"n"_2/"n"_1` - From the Right angle triangle ∆ ABC,
sin ic = `"CB"/"AB" = "R"/sqrt("d"^2 + "R"^2)`
Equating the above two equations
`"R"/sqrt("d"^2 + "R"^2) = ("n"_2/"n"_1)`
Radius of Snell’s window
Squaring on both sides,
`"R"^2/("R"^2 + "d"^2) = ("n"_2/"n"_1)^2`
Taking reciprocal,
`("R"^2 + "d"^2)/"R"^2 = ("n"_1/"n"_2)^2`
On further simplifying,
`1 + "d"^2/"R"^2 = ("n"_1/"n"_2)^2; "d"^2/"R"^2 = ("n"_1/"n"_2)^2 - 1;`
`"d"^2/"R"^2 = ("n"_1^2/"n"_2^2) - 1 = ("n"_1^2 - "n"_2^2)/"n"_2^2`
Again taken reciprocal and rearranging
`"R"^2/"R"^2 = "n"_2^2/("n"_1^2 - "n"_2^2); "R"^2 = "d"^2("n"_2^2/("n"_1^2 - "n"_2^2))`
Tha radius of illumination is,
R = d`sqrt(("n"_2^2)/("n"_1^2 - "n"_2^2))`
If the rarer medium outside in air, then, n2 = 1, and we can take n1 = n
R = d`1/sqrt("n"^2 - 1)` (or) R = `"d"/sqrt("n"^2 - 1)`
APPEARS IN
संबंधित प्रश्न
A converging lens has a focal length of 20 cm in air. It is made of a material of refractive index 1·6. If it is immersed in a liquid of refractive index 1·3, find its new focal length.
A narrow beam of white light goes through a slab having parallel faces.
(a) The light never splits in different colours
(b) The emergent beam is white
(c) The light inside the slab is split into different colours
(d) The light inside the slab is white
An object P is focussed by a microscope M. A glass slab of thickness 2.1 cm is introduced between P and M. If the refractive index of the slab is 1.5, by what distance should the microscope be shifted to focus the object again?
A vessel contains water up to a height of 20 cm and above it an oil up to another 20 cm. The refractive indices of the water and the oil are 1.33 and 1.30 respectively. Find the apparent depth of the vessel when viewed from above.
Consider the situation in figure. The bottom of the pot is a reflecting plane mirror, S is a small fish and T is a human eye. Refractive index of water is μ. (a) At what distance(s) from itself will the fish see the image(s) of the eye? (b) At what distance(s) from itself will the eye see the image(s) of the fish.

Locate the image formed by refraction in the situation shown in figure.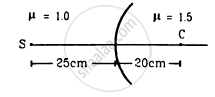
Obtain the equation for apparent depth.
What is critical angle and total internal reflection?
If `"^imu_j` represents refractive index, when a light ray goes from medium i to medium j, then the product `"^2mu_1 xx ^3mu_2 xx ^4mu_3` is equal to ______.
