Advertisements
Advertisements
प्रश्न
Using identity, find the value of (100.1)2
उत्तर
(100.1)2 = (100 + 0.1)2
Substituting a = 100 and b = 0.1 in
(a + b)2 = a2 + 2ab + b2, we have
(100 + 0.1)2 = (100)2 + 2(100)(0.1) + (0.1)2
(100.1)2 = 10000 + 20 + 0.01
(100.1)2 = 10020.01
APPEARS IN
संबंधित प्रश्न
Use a suitable identity to get the following products.
(7a − 9b) (7a − 9b)
Using identities, evaluate 992
Using identities, evaluate 9982
Expand `("x"+1/2)^2`
Use an expansion formula to find the value.
(997)2
Use a formula to multiply of (2a – 13)(2a + 13)
Factorise the following.
x2 + 9x + 20
If a2 + b2 = 74 and ab = 35, then find a + b.
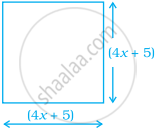
Find the length of the side of the given square if area of the square is 625 square units and then find the value of x.
Take suitable number of cards given in the adjoining diagram [G(x × x) representing x2, R(x × 1) representing x and Y(1 × 1) representing 1] to factorise the following expressions, by arranging the cards in the form of rectangles:
- 2x2 + 6x + 4
- x2 + 4x + 4.
Factorise 2x2 + 6x + 4 by using the figure.
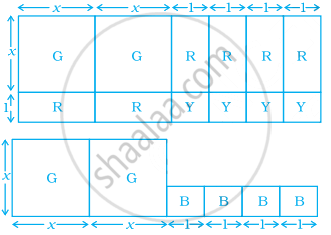
Calculate the area of figure.
