Advertisements
Advertisements
प्रश्न
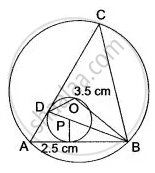
Using ruler and compass only, construct a triangle ABC such that AB = 5 cm, ABC = 75°, and the radius of the circumcircle of triangle ABC is 3.5 cm. On the same diagram, construct a circle, touching AB at its middle point and also touching the side AC.
उत्तर
Steps:
Draw a line segment AB = 5 cm long. Make an angle of 75° at 'B' draw perpendicular bisector of AB and the angular bisector of B.
Make 3.5 cm on the perpendicular bisector with O as centre and radius equal to OA or OB draw circumcircle. Mark 2.5 cm on AC from A. Join BD, it will intersect at P, with P as centre and PD as radius draw another circle.
APPEARS IN
संबंधित प्रश्न
Construct a regular hexagon of side 5 cm. Hence construct all its lines of symmetry and name them.
Using a ruler and compasses only:
1) Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ABC = 120°
2) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
3) Measure ∠BCP.
Construct a triangle ABC in which base BC = 6 cm, AB = 5.5 cm and ∠ABC = 120°.
Construct a circle circumscribing the triangle ABC.
Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Using a ruler and compasses only:
- Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ∠ABC = 120°.
- In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
- Measure ∠BCP.
Draw a circle of radius 2. 5 cm and circumscribe a square about it.
Draw a line segment OA , 5 cm long. AT O , using ruler and compasses only, construct OB such that , ∠ AOB = 37.5° construct a circle to touch OA at A and to touch OB at B.
Draw line segments OA = 4.5 cm, OB = 3.2 cm such that ∠ AOB = 45°. Construct a circle touching OA at A and passing through B.
Construct a triangle ABC in which AB = 5 cm, BC = 6.8 cm and median AD = 4.4 cm. Draw incircle of this triangle.
In triangle ABC, ∠ABC = 90°, AB = 6 cm, BC = 7.2 cm and BD is perpendicular to side AC. Draw circumcircle of triangle BDC and then state the length of the radius of this circumcircle drawn.
Use ruler and compasses only for this question:
(i) Construct A ABC, where AB = 3.5 cm, BC = 6 cm and ∠ ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC, and also equidistant from B and C. Measure and record the length of PB.
