Advertisements
Advertisements
प्रश्न
Using a ruler and compasses only:
- Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ∠ABC = 120°.
- In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
- Measure ∠BCP.
उत्तर
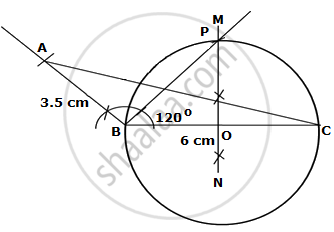
Steps of construction:
- Draw a line segment BC = 6 cm.
At B, draw a ray BX making an angle of 120° with BC. with B as center and radius 3.5 cm, out off AB = 3.5 cm. Join AC
Thus, ABC is the required triangle. - Draw perpendicular bisector MN of BC at point O. With O as center and radius = OB, draw a cirde.
Draw angle bisector of ∠ABC which meets the circle at point P.
Thus, point P is equidistant from AB and BC. - On mesuring, ∠BCP = 30°
APPEARS IN
संबंधित प्रश्न
Construct a ΔABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle.
Using a ruler and compasses only:
1) Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ABC = 120°
2) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
3) Measure ∠BCP.
Constuct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°. Hence:
- Construct the locus of point equdistant from BA and BC.
- Construct the locus of points equidistant from B and C.
- Mark the point which satisfies the above two loci as P. Measure and write the length of PC.
Construct Δ ABC in which AB = 5 cm, BC = 4. 5 cm and ∠ ABC = 60" .. Construct a cirde to circumscribe. Δ ABC.
Using ruler and compasses only, construct and equilateral triangle with side 4.5 cm. Draw a circumcircle of this triangle and measure its radius.
Draw a circle with radius 3 cm and inscribe an equilateral triangle in it.
Draw a line segment OA , 5 cm long. AT O , using ruler and compasses only, construct OB such that , ∠ AOB = 37.5° construct a circle to touch OA at A and to touch OB at B.
Construct a triangle ABC in which AB = 5 cm, BC = 6.8 cm and median AD = 4.4 cm. Draw incircle of this triangle.
In triangle ABC, ∠ABC = 90°, AB = 6 cm, BC = 7.2 cm and BD is perpendicular to side AC. Draw circumcircle of triangle BDC and then state the length of the radius of this circumcircle drawn.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
