Advertisements
Advertisements
प्रश्न
Using vectors, find the value of k such that the points (k, – 10, 3), (1, –1, 3) and (3, 5, 3) are collinear.
उत्तर
Let the given points are A(k, 10, 3), B(1, 1, 3) and C(3, 5, 3)
`vec"AB" = (1 - "k")hat"i" + (-1 + 10)hat"j" + (3 - 3)hat"k"`
`vec"AB" = (1 - "k")hat"i" + 9hat"j" + 0hat"k"`
∴ `|vec"AB"| = sqrt((1 - "k")^2 + (9)^2)`
= `sqrt((1 - "k")^2 + 81)`
`vec"BC" = (3 - 1)hat"i" + (5 + 1)hat"j" + (3 - 3)hat"k"`
= `2hat"i" + 6hat"j" + 0hat"k"`
∴ `|vec"BC"| = sqrt((2)^2 + (6)^2)`
= `sqrt(4 + 36)`
= `sqrt(40)`
= `2sqrt(10)`
`vec"AC" = (3 - "k")hat"i" + (5 + 10)hat"j" + (3 - 3)hat"k"`
= `(3 - "k")hat"i" + 15hat"j" + 0hat"k"`
∴ `|vec"AC"| = sqrt((3 - "k")^2 + (15)^2)`
= `sqrt((3 - "k")^2 + 225)`
If A, B and C are collinear, then
`|vec"AB"| + |vec"BC"| = |vec"AC"|`
`sqrt((1 - "k")^2 + 81) + sqrt(40) = sqrt((3 - "k")^2 + 225)`
Squaring both sides, we have
`[sqrt((1 - "k")^2 + 81) + sqrt(40)]^2 = [sqrt((3 - "k")^2 + 225)]^2`
⇒ `(1 - "k")^2 + 81 + 40 + 2sqrt(40) sqrt((1 - "k")^2 + 81) = (3 - "k")^2 + 225`
⇒ `1 + "k"^2 - 2"k" + 121 + 2sqrt(40) sqrt(1 + "k"^2 - 2"k" + 81) =9 + "k"^2 - 6"k" + 225`
⇒ `122 - 2"k" + 2sqrt(40) sqrt("k"^2 - 2"k" + 82) = 234 - 6"k"`
Dividing by 2, we get
⇒ `61 - "k" + sqrt(40) sqrt("k"^2 - 2"k" + 82) = 117 - 3"k"`
⇒ `sqrt(40) sqrt("k"^2 - 2"k" + 82) = 117 - 61 - 3"k" + "k"`
⇒ `sqrt(40) sqrt("k"^2 - 2"k" + 82) = 56 - 2"k"`
⇒ `sqrt(10) sqrt("k"^2 - 2"k" + 82) = 28 - "k"` ...(Dividing by 2)
Squaring both sides, we get
⇒ 10(k2 – 2k + 82) = 784 + k2 – 56k
⇒ 10k2 – 20k + 820 = 784 + k2 – 56k
⇒ 10k2 – k2 – 20k + 56k + 820 – 784 = 0
⇒ 9k2 + 36k + 36 = 0
⇒ k2 + 4k + 4 = 0
⇒ (k + 2)2 = 0
⇒ k = – 2
⇒ k = – 2
Hence, the required value is k = – 2
APPEARS IN
संबंधित प्रश्न
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] represent the sides of a triangle taken in order, then write the value of \[\vec{a} + \vec{b} + \vec{c} .\]
Write a unit vector making equal acute angles with the coordinates axes.
Write the position vector of a point dividing the line segment joining points A and B with position vectors \[\vec{a}\] and \[\vec{b}\] externally in the ratio 1 : 4, where \[\overrightarrow{a} = 2 \hat{i} + 3 \hat{j} + 4 \hat{k} \text{ and }\overrightarrow{b} = - \hat{i} + \hat{j} + \hat{k} .\]
If \[\left| \overrightarrow{a} \right| = 4\] and \[- 3 \leq \lambda \leq 2\], then write the range of \[\left| \lambda \vec{a} \right|\].
Find the components along the coordinate axes of the position vector of the following point :
S(4, –3)
Find the position vector of the mid-point of the vector joining the points
ABCDEF is a regular hexagon. Show that `bar"AB" + bar"AC" + bar"AD" + bar"AE" + bar"AF" = 6bar"AO"`, where O is the centre of the hexagon.
Check whether the vectors `2hati + 2hatj + 3hatk, - 3hati + 3hatj + 2hatk` and `3hati + 4hatk` form a triangle or not.
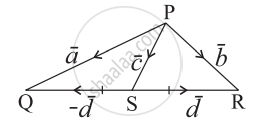
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Select the correct option from the given alternatives:
Let a, b, c be distinct non-negative numbers. If the vectors `"a"hat"i" + "a"hat"j" + "c"hat"k" , hat"i" + hat"k" "and" "c"hat"i" + "c"hat"j" + "b"hat"k"` lie in a plane, then c is
Select the correct option from the given alternatives:
If `bar"a", bar"b", bar"c"` are non-coplanar unit vectors such that `bar"a"xx (bar"b"xxbar"c") = (bar"b"+bar"c")/sqrt2`, then the angle between `bar"a" "and" bar"b"` is
If `|bar"a"| = |bar"b"| = 1, bar"a".bar"b" = 0, bar"a" + bar"b" + bar"c" = bar"0", "find" |bar"c"|`.
If ABC is a triangle whose orthocentre is P and the circumcentre is Q, prove that `bar"PA" + bar"PB" + bar"PC" = 2bar"PQ".`
Express `hat"i" + 4hat"j" - 4hat"k"` as the linear combination of the vectors `2hat"i" - hat"j" + 3hat"k", hat"i" - 2hat"j" + 4hat"k"` and `- hat"i" + 3hat"j" - 5hat"k"`.
Let bar"b" = 4hat"i" + 3hat"j" and bar"c" be two vectors perpendicular to each other in the XY-plane. Find the vector in the same plane having projection 1 and 2 along bar"b" and bar"c" respectively.
Show that the vector area of a triangle ABC, the position vectors of whose vertices are `bar"a", bar"b" and bar"c"` is `1/2[bar"a" xx bar"b" + bar"b" xx bar"c" + bar"c" xx bar"a"]`.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b" xx bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b") xx (bar"c".bar"d")`
For any non zero vector, a, b, c a · ((b + c) × (a + b + c)] = ______.
Find a vector `vec"r"` of magnitude `3sqrt(2)` units which makes an angle of `pi/4` and `pi/2` with y and z-axes, respectively.
Classify the following measures as scalar and vector.
20 m/s2
Let `bara, barb` and `barc` be three vectors, then `bara xx (barb xx barc) = (bara xx barb) xx barc` if
If two or more vectors are parallel to the same line, such vectors are known as:
Let the vectors `vec(a)` such `vec(b)` that `|veca|` = 3 and `|vecb| = sqrt(2)/3`, then `veca xx vecb` is a unit vector if the angle between `veca` and `vecb` is
If points P(4, 5, x), Q(3, y, 4) and R(5, 8, 0) are collinear, then the value of x + y is ______.
In the triangle PQR, `bar(PQ) = 2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bar a and bar b `.
- `bar("PR")`
- `bar("PM")`
- `bar("QM")`
Evaluate the following.
`int x^3/(sqrt1 + x^4) `dx
In the triangle PQR, `bar"PQ" = 2 bar" a" and bar"QR" = 2 bar"b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`
Check whether the vectors `2hati + 2hatj +3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
