Advertisements
Advertisements
प्रश्न
If \[\left| \overrightarrow{a} \right| = 4\] and \[- 3 \leq \lambda \leq 2\], then write the range of \[\left| \lambda \vec{a} \right|\].
उत्तर
We have `|vec∝| = 4 and -3 <= lambda <= 2`
∴ `|lambda veca| = |- 3| 4 = 12, at lambda = - 3`
`|lambda veca| = |0| 4 = 0, at lambda = 0`
And `|lambda vec∝| |2| 4 = 8, at lambda = 2`
So, the range of `|lambda vec∝| is [0, 12].`
Alternate Method
Since, `- 3 <= lambda <= 2`
`0 <= || lambda| <= 3`
`= 0 <= 4| lambda| <= 12`
`|lambda veca| ∈ [0, 12]`
APPEARS IN
संबंधित प्रश्न
if `veca = 2hati - hatj - 2hatk " and " vecb = 7hati + 2hatj - 3hatk`, , then express `vecb` in the form of `vecb = vec(b_1) + vec(b_2)`, where `vec(b_1)` is parallel to `veca` and `vec(b_2)` is perpendicular to `veca`
Write a unit vector in the direction of \[\overrightarrow{b} = 2 \hat{i} + \hat{j} + 2 \hat{k}\].
If three points A, B and C have position vectors \[\hat{i} + x \hat{j} + 3 \hat{k} , 3 \hat{i} + 4 \hat{j} + 7 \hat{k}\text{ and }y \hat{i} - 2 \hat{j} - 5 \hat{k}\] respectively are collinear, then (x, y) =
Find the vector equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0. Hence find whether the plane thus obtained contains the line \[\frac{x + 2}{5} = \frac{y - 3}{4} = \frac{z}{5}\] or not.
In the triangle PQR, `bar"PQ" = bar"2a", bar"QR" = bar"2b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`.
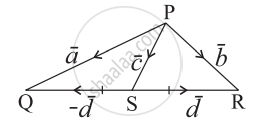
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
Find a vector in the direction of `bara = hati - 2hatj` that has magnitude 7 units.
Find the coordinates of the point which is located three units behind the YZ-plane, four units to the right of XZ-plane, and five units above the XY-plane.
Find the coordinates of the point which is located in the YZ-plane, one unit to the right of the XZ- plane, and six units above the XY-plane.
Find the area of the traingle with vertices (1, 1, 0), (1, 0, 1) and (0, 1, 1).
Select the correct option from the given alternatives:
The value of `hat"i".(hat"j" xx hat"k") + hat"j".(hat"i" xx hat"k") + hat"k".(hat"i" xx hat"j")` is
If two sides of a triangle are `hat"i" + 2hat"j" and hat"i" + hat"k"`, find the length of the third side.
Find the lengths of the sides of the triangle and also determine the type of a triangle:
L (3, -2, -3), M (7, 0, 1), N(1, 2, 1).
If P is orthocentre, Q is the circumcentre and G is the centroid of a triangle ABC, then prove that `bar"QP" = 3bar"QG"`.
Find two unit vectors each of which makes equal angles with bar"u", bar"v" and bar"w" where bar"u" = 2hat"i" + hat"j" - 2hat"k", bar"v" = hat"i" + 2hat"j" - 2hat"k", bar"w" = 2hat"i" - 2hat"j" + hat"k".
Express `hat"i" + 4hat"j" - 4hat"k"` as the linear combination of the vectors `2hat"i" - hat"j" + 3hat"k", hat"i" - 2hat"j" + 4hat"k"` and `- hat"i" + 3hat"j" - 5hat"k"`.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b" xx bar"c")`
If `bar"a", bar"b", bar"c"` are three non-coplanar vectors show that `(bar"a".(bar"b" xx bar"c"))/((bar"c" xx bar"a").bar"b") + (bar"b".(bar"a" xx bar"c"))/((bar"c" xx bar"a").bar"b") = 0`
For any non-zero vectors a and b, [b a × b a] = ?
If A, B, C and D are (3, 7, 4), (5, -2, - 3), (- 4, 5, 6) and(1, 2, 3) respectively, then the volume of the parallelopiped with AB, AC and AD as the co-terminus edges, is ______ cubic units.
If the points (–1, –1, 2), (2, m, 5) and (3,11, 6) are collinear, find the value of m.
The vector with initial point P (2, –3, 5) and terminal point Q(3, –4, 7) is ______.
The area of the parallelogram whose adjacent sides are `hat"i" + hat"k"` and `2hat"i" + hat"j" + hat"k"` is ______.
If `veca` and `vecb` are unit vectors, then what is the angle between `veca` and `vecb` for `sqrt(3) veca - vecb` to be a unit vector?
If `|vec"a" + vec"b"| = |vec"a" - vec"b"|`, then the vectors `vec"a"` and `vec"b"` are orthogonal.
If `vec"a"` and `vec"b"` are adjacent sides of a rhombus, then `vec"a" * vec"b"` = 0
Classify the following as scalar and vector quantity.
Distance
Classify the following as scalar and vector quantity.
Velocity
In Figure, identify the following vector.

Equal
Let `veca, vecb` and `vecc` be three unit vectors such that `veca xx (vecb xx vecc) = sqrt(3)/2 (vecb + vecc)`. If `vecb` is not parallel to `vecc`, then the angle between `veca` and `vecc` is
`bara, barb` and `barc` are three vectors such that `veca + vecb + vecc` 20, `|bara| = 1, |barb| = 2` and `|barc| = 3`. Then `bara. barb + barb.barc + bar(c.a)` is equal to
Four vectors `veca, vecb, vecc` and `vecx` satisfy the relation `(veca.vecx)vecb = vecc + vecx` where `vecb * veca` ≠ 1. The value of `vecx` in terms of `veca, vecb` and `vecc` is equal to
For given vectors, `veca = 2hati - hatj + 2hatk` and `vecb = - hati + hatj - hatk` find the unit vector in the direction of the vector `veca + vecb`.
Unit vector along `vec(PQ)`, where coordinates of P and Q respectively are (2, 1, – 1) and (4, 4, – 7), is ______.
Check whether the vectors `2hati+2hatj+3hatk,-3hati+3hatj+2hatk` and `3hati+4hatk` form a triangle or not.
Evaluate the following.
`int x^3/(sqrt1 + x^4) `dx
In the triangle PQR, `bar(PQ)=2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bara and barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
In the triangle PQR, `bar"PQ" = bar"2a", bar"QR" = bar"2b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`.
