Advertisements
Advertisements
प्रश्न
In a triangle OAC, if B is the mid-point of side AC and \[\overrightarrow{OA} = \overrightarrow{a} , \overrightarrow{OB} = \overrightarrow{b}\], then what is \[\overrightarrow{OC}\].
उत्तर
In ∆OAC, \[\overrightarrow{OA} = \overrightarrow{a}\] and \[\overrightarrow{OB} = \overrightarrow{b}\]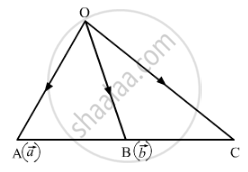
It is given that B is the mid-point of AC.
∴ Position vector of B = \[\frac{\text{ Position vector of A + Position vector of C }}{2}\]
\[\Rightarrow \overrightarrow{OB} = \frac{\overrightarrow{OA} + \overrightarrow{OC}}{2}\]
\[ \Rightarrow \overrightarrow{b} = \frac{\overrightarrow{a} + \overrightarrow{OC}}{2}\]
\[ \Rightarrow \overrightarrow{a} + \overrightarrow{OC} = 2 \overrightarrow{b} \]
\[ \Rightarrow \overrightarrow{OC} = 2 \overrightarrow{b} - \overrightarrow{a}\]
APPEARS IN
संबंधित प्रश्न
Write a unit vector making equal acute angles with the coordinates axes.
If \[\overrightarrow{a} = \hat{i} + \hat{j} , \overrightarrow{b} = \hat{j} + \hat{k} , \overrightarrow{c} = \hat{k} + \hat{i}\], find the unit vector in the direction of \[\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}\].
If \[\overrightarrow{a} = x \hat{i} + 2 \hat{j} - z \hat{k}\text{ and }\overrightarrow{b} = 3 \hat{i} - y \hat{j} + \hat{k}\] are two equal vectors, then write the value of x + y + z.
If ABCDEF is a regular hexagon, then \[\overrightarrow{AD} + \overrightarrow{EB} + \overrightarrow{FC}\] equals
The position vectors of the points A, B, C are \[2 \hat{i} + \hat{j} - \hat{k} , 3 \hat{i} - 2 \hat{j} + \hat{k}\text{ and }\hat{i} + 4 \hat{j} - 3 \hat{k}\] respectively.
These points
Find a vector in the direction of `bara = hati - 2hatj` that has magnitude 7 units.
Find the coordinates of the point which is located three units behind the YZ-plane, four units to the right of XZ-plane, and five units above the XY-plane.
If the sum of two unit vectors is itself a unit vector, then the magnitude of their difference is ______.
If `|bara|` = 3, `|barb|` = 5, `|barc|` = 7 and `bara + barb + barc = bar0`, then the angle between `bara` and `barb` is ______.
Select the correct option from the given alternatives:
If l, m, n are direction cosines of a line then `"l"hat
"i" + "m"hat"j" + "n"hat"k"` is ______
Select the correct option from the given alternatives:
Let α, β, γ be distinct real numbers. The points with position vectors `alphahat"i" + betahat"j" + gammahat"k", betahat"i" + gammahat"j" + alphahat"k", gammahat"i" + alphahat"j" + betahat"k"`
ABCD is a parallelogram. E, F are the midpoints of BC and CD respectively. AE, AF meet the diagonal BD at Q and P respectively. Show that P and Q trisect DB.
Show that no line in space can make angles `pi/6` and `pi/4` with X-axis and Y-axis.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`(bar"a".bar"b") xx (bar"c".bar"d")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`|bar"a"|(bar"b".bar"c")`
For any vectors `bar"a", bar"b", bar"c"` show that `(bar"a" + bar"b" + bar"c") xx bar"c" + (bar"a" + bar"b" + bar"c") xx bar"b" + (bar"b" - bar"c") xx bar"a" = 2bar"a" xx bar"c"`
If `bar"a", bar"b", bar"c"` are three non-coplanar vectors show that `(bar"a".(bar"b" xx bar"c"))/((bar"c" xx bar"a").bar"b") + (bar"b".(bar"a" xx bar"c"))/((bar"c" xx bar"a").bar"b") = 0`
For any non-zero vectors a and b, [b a × b a] = ?
a and b are non-collinear vectors. If p = (2x + 1) a - band q = (x - 2)a +b are collinear vectors, then x = ______.
If A, B, C and D are (3, 7, 4), (5, -2, - 3), (- 4, 5, 6) and(1, 2, 3) respectively, then the volume of the parallelopiped with AB, AC and AD as the co-terminus edges, is ______ cubic units.
Find a vector of magnitude 11 in the direction opposite to that of `vec"PQ"` where P and Q are the points (1, 3, 2) and (–1, 0, 8), respectively.
The unit vector perpendicular to the vectors `hat"i" - hat"j"` and `hat"i" + hat"j"` forming a right handed system is ______.
If `vec"a", vec"b", vec"c"` are unit vectors such that `vec"a" + vec"b" + vec"c"` = 0, then the value of `vec"a" * vec"b" + vec"b" * vec"c" + vec"c" * vec"a"` is ______.
The values of k for which `|"k"vec"a"| < |vec"a"|` and `"k"vec"a" + 1/2 vec"a"` is parallel to `vec"a"` holds true are ______.
Classify the following measures as scalar and vector.
40°
Classify the following measures as scalar and vector.
10-19 coulomb
Classify the following as scalar and vector quantity.
Force
If `veca ≠ vec(0), veca.vecb = veca.vecc, veca xx vecb = veca xx vecc`, then show that `vecb = vecc`.
The unit vector perpendicular to the vectors `6hati + 2hatj + 3hatk` and `3hati - 6hatj - 2hatk` is
If points P(4, 5, x), Q(3, y, 4) and R(5, 8, 0) are collinear, then the value of x + y is ______.
In the triangle PQR, `bar(PQ)` = `2bara` and `bar(QR)` = `2barb`. The mid-point of PR is M. Find following vectors in terms of `bara` and `barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
Check whether the vectors `2hati +2hatj+3hatk, -3hati +3hatj +2hatk and 3hati +4hatk` form a triangle or not.
In the triangle PQR, `bb(bar(PQ) = 2 bara)` and `bb(bar(QR) = 2 barb)`. The mid-point of PR is M. Find the following vectors in terms of `bb(bara and barb)`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
In the triangle PQR, `bar(PQ)=2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bara and barb`.
(i) `bar(PR)` (ii) `bar(PM)` (iii) `bar(QM)`
In the triangle PQR, `bar"PQ" = 2 bar" a" and bar"QR" = 2 bar"b"`. The midpoint of PR is M. Find the following vectors in terms of `bar"a"` and `bar"b"`:
(i) `bar"PR"` (ii) `bar"PM"` (iii) `bar"QM"`
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
