Advertisements
Advertisements
प्रश्न
Value of universal gas constant (R) is same for all gases. What is its physical significance?
उत्तर
Unit of R depends on the units of p, V and T are measured, We know, `R = (pV)/(nT)`
Now, let's say, the pressure is measured in Pascal, per mole volume is measured in m3 and temperature is measured in Kelvin, then. Units of ‘R’ are Pa m3K–1 mol–1. Also, R is work done per mole per kelvin. It’s unit is J K–1 mol–1 (Joule is the unit of work done).
APPEARS IN
संबंधित प्रश्न
Calculate the volume occupied by 8.8 g of CO2 at 31.1°C and 1 bar pressure. R = 0.083 bar L K–1 mol–1.
The value of the universal gas constant depends upon
In what way real gases differ from ideal gases.
Explain whether a gas approaches ideal behavior or deviates from ideal behaviour if it is compressed to a smaller volume at a constant temperature.
Write the Van der Waals equation for a real gas. Explain the correction term for pressure and volume.
A plot of volume (V) versus temperature (T) for a gas at constant pressure is a straight line passing through the origin. The plots at different values of pressure are shown in Figure. Which of the following order of pressure is correct for this gas?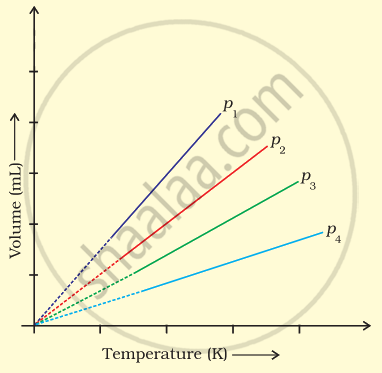
If 1 gram of each of the following gases are taken at STP, which of the gases will occupy (a) greatest volume and (b) smallest volume?
\[\ce{CO, H2O, CH4 , NO}\]
Compressibility factor, Z, of a gas is given as Z = `(pV)/(nRT)`. For real gas what will be the effect on value of Z above Boyle’s temperature?
Pressure versus volume graph for a real gas and an ideal gas are shown in figure. Answer the following questions on the basis of this graph.
(i) Interpret the behaviour of real gas with respect to ideal gas at low pressure.
(ii) Interpret the behaviour of real gas with respect to ideal gas at high pressure.
(iii) Mark the pressure and volume by drawing a line at the point where real gas behaves as an ideal gas.
Match the following graphs of ideal gas with their co-ordinates:
| Graphical representation | x and y co-ordinates |
(i)  |
(a) pV vs. V |
(ii) 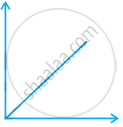 |
(b) p vs. V |
(iii) 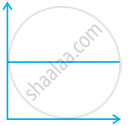 |
(c) p vs. `1/V` |
