Advertisements
Advertisements
प्रश्न
Verify the Ampere’s law for magnetic field of a point dipole of dipole moment m = m`hatk`. Take C as the closed curve running clockwise along (i) the z-axis from z = a > 0 to z = R; (ii) along the quarter circle of radius R and centre at the origin, in the first quadrant of x-z plane; (iii) along the x-axis from x = R to x = a, and (iv) along the quarter circle of radius a and centre at the origin in the first quadrant of x-z plane.
उत्तर
Consider a plane on x-z plane on which there are two loops (of radius R and a)and a point dipole on origin of dipole moment M(as shown in the figure). From P to Q, every point on the z-axis lies at the axial line of magnetic dipole of moment M.
So magnetic field induction (B) at a point (0, 0, z) from magnetic dipole (centre at origin) and having magnetic moment `vecm hatk` of magnitude `(vecm)`.
`|B| = mu_0/(4pi) (2(vecm))/z^3 = (mu_0vecm)/(2piz^3)`
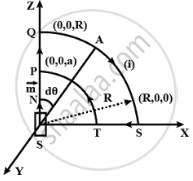
(i) Ampere's law along Z axis from Z = a to Z = R i.e. from P to Q
`int_P^Q vecB.vec(dl) = int_P^Q B.dl cos θ^circ = int_P^Q B.dz`
= `int_P^Q (mu_0vecm)/(2piz^3) dz = (mu_0vecm)/(2pi) int_a^R z^(-3) dz` .....[∵ Distance of P and Q from origin are a and R respectively]
= `(mu_0vecm)/(2pi) [z^-2/(-2)]_a^R = (mu_0vecm)/(2pi(-2)) [1/R^2 - 1/a^2]`
`int_P^Q B.dl = (mu_0vecm)/(4pi) [1/a^2 - 1/R^2]`
(ii) Ampere's law along the quarter circle QS of radius R as given in figure here. Point A can be considered on the equatorial line of magnetic dipole of moment `vecm` sin θ.
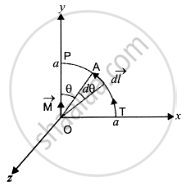
Magnetic field of point A on the circular are is
`B = mu_0/(4pi) (vecm sin theta)/R^3`
`d theta = (dl)/R` ⇒ `R.d theta`
∴ By Ampere's law `int B.dl = int B.dl cos theta`
`int vecB. vec(dl) = int_0^(pi/2) mu_0/(4pi) (vecm sin theta)/R^3 * R.d theta`
`int vecB.vec(dl) = (mu_0vecm)/(4piR^2) [- cos theta]_0^(pi/2) = (mu_0vecm)/(4piR^2) [- cos 90^circ + cos theta^circ]`
`int B.dl = (mu_0vecm)/(4piR^2)`
(iii) Ampere's law along the X-axis from x = R to x = a as in given figure here.

As all point from S to T lies on equatorial line of magnetic dipole N-S. So magnetic field induction at a point P at a distance x from the dipole is
`B = mu_0/(4pi x^3) = mu_0/(4pi) (vecm hatk)/x^3`
`int vecB.vec(dl) = int_R^q (- mu_0 vecmhatk)/(4 pix^3) * vec(dl)`
∵ Angle between dl and m is 90°
So `int vecB.vec(dl) = int_R^a (- mu_0 |vecm| dl cos 90^circ)/(4pix^3)` = 0
`B = mu_0/(4pi) vecm/x^3 = mu_0/(4pi) (vecm hatk)/x^3`
`int vecB.vec(dl) = int_R^a (- mu_0 vecmhatk)/(4pix^3) * vec(dl)`
∵ Angle between dl and m is 90°
So `int vecB.vec(dl) = int_R^a (- mu_0 |vecm| dl cos 90^circ)/(4pix^3)` = 0
(iv) Ampere's law along the quarter circle of radius 'a' and centre at the origin in the quadrant X-z plane as in figure here as on part (ii).
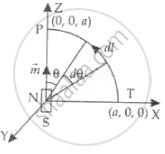
`int B.dl = int_(pi/2)^0 mu_0/(4pi) (vecm sin theta)/a^3 * ad theta`
`int B.dl = (mu_0vecm)/(4pia^2) [- cos theta]_(pi/2)^0`
θ = angle from axial line of dipole
`int B.dl = (mu_0vecm)/(4pia) [- cos theta + cos pi/2] = (mu_0vecm)/(4pia^2) (-1 + 0) = (-mu_0vecm)/(4pia^2)`
∴ Applying Ampere's law along close path starting from P to Q, Q to S and S to P.
`oint_(PQST) B.dl = int_P^Q vecB. vec(dl) + int_Q^S vecB.vec(dl) + int_S^T vecB. vec(dl) + int_T^P B.dl`
From parts (i), (ii), (iii) and (iv) substituting the values
`oint_(PQST) B.dl = (mu_0vecm)/(4pi) (1/a^2 - 1/R^2) + (mu_0vecm)/(4piR^2) + 0 + (-mu_0vecm)/(4pia^2)`
= `(mu_0vecm)/(4pia^2) - (mu_0vecm)/(4piR^2) + (mu_0vecm)/(4piR) - (mu_0vecm)/(4pia^2)`
`oint_(PQST) B.dl` = 0
This proves that Ampere's law is magnetism.
APPEARS IN
संबंधित प्रश्न
An iron needle is attracted to the ends of a bar magnet but not to the middle region of the magnet. Is the material making up the ends of a bare magnet different from that of the middle region?
Answer the following question.
Write the four important properties of the magnetic field lines due to a bar magnet.
Answer the following question in detail.
A circular magnet is made with its north pole at the centre, separated from the surrounding circular south pole by an air gap. Draw the magnetic field lines in the gap.
Answer the following question in detail.
Two bar magnets are placed on a horizontal surface. Draw magnetic lines around them. Mark the position of any neutral points (points where there is no resultant magnetic field) on your diagram.
A closely wound solenoid of 800 turns and area of cross-section 2.5 × 10–4 m2 carries a current of 3.0 A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment?
When iron filings are sprinkled on a sheet of glass placed over a short bar magnet then, the iron filings form a pattern suggesting that the magnet has ______.
Magnetic field at far axial point due to solenoid as well as bar magnet varies ______.
A toroid of n turns, mean radius R and cross-sectional radius a carries current I. It is placed on a horizontal table taken as x-y plane. Its magnetic moment m ______.
A proton has spin and magnetic moment just like an electron. Why then its effect is neglected in magnetism of materials?
