Advertisements
Advertisements
प्रश्न
Verify the Ampere’s law for magnetic field of a point dipole of dipole moment m = m`hatk`. Take C as the closed curve running clockwise along (i) the z-axis from z = a > 0 to z = R; (ii) along the quarter circle of radius R and centre at the origin, in the first quadrant of x-z plane; (iii) along the x-axis from x = R to x = a, and (iv) along the quarter circle of radius a and centre at the origin in the first quadrant of x-z plane.
उत्तर
Consider a plane on x-z plane on which there are two loops (of radius R and a)and a point dipole on origin of dipole moment M(as shown in the figure). From P to Q, every point on the z-axis lies at the axial line of magnetic dipole of moment M.
So magnetic field induction (B) at a point (0, 0, z) from magnetic dipole (centre at origin) and having magnetic moment `vecm hatk` of magnitude `(vecm)`.
`|B| = mu_0/(4pi) (2(vecm))/z^3 = (mu_0vecm)/(2piz^3)`
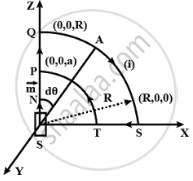
(i) Ampere's law along Z axis from Z = a to Z = R i.e. from P to Q
`int_P^Q vecB.vec(dl) = int_P^Q B.dl cos θ^circ = int_P^Q B.dz`
= `int_P^Q (mu_0vecm)/(2piz^3) dz = (mu_0vecm)/(2pi) int_a^R z^(-3) dz` .....[∵ Distance of P and Q from origin are a and R respectively]
= `(mu_0vecm)/(2pi) [z^-2/(-2)]_a^R = (mu_0vecm)/(2pi(-2)) [1/R^2 - 1/a^2]`
`int_P^Q B.dl = (mu_0vecm)/(4pi) [1/a^2 - 1/R^2]`
(ii) Ampere's law along the quarter circle QS of radius R as given in figure here. Point A can be considered on the equatorial line of magnetic dipole of moment `vecm` sin θ.
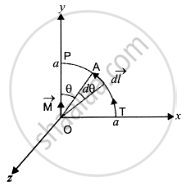
Magnetic field of point A on the circular are is
`B = mu_0/(4pi) (vecm sin theta)/R^3`
`d theta = (dl)/R` ⇒ `R.d theta`
∴ By Ampere's law `int B.dl = int B.dl cos theta`
`int vecB. vec(dl) = int_0^(pi/2) mu_0/(4pi) (vecm sin theta)/R^3 * R.d theta`
`int vecB.vec(dl) = (mu_0vecm)/(4piR^2) [- cos theta]_0^(pi/2) = (mu_0vecm)/(4piR^2) [- cos 90^circ + cos theta^circ]`
`int B.dl = (mu_0vecm)/(4piR^2)`
(iii) Ampere's law along the X-axis from x = R to x = a as in given figure here.

As all point from S to T lies on equatorial line of magnetic dipole N-S. So magnetic field induction at a point P at a distance x from the dipole is
`B = mu_0/(4pi x^3) = mu_0/(4pi) (vecm hatk)/x^3`
`int vecB.vec(dl) = int_R^q (- mu_0 vecmhatk)/(4 pix^3) * vec(dl)`
∵ Angle between dl and m is 90°
So `int vecB.vec(dl) = int_R^a (- mu_0 |vecm| dl cos 90^circ)/(4pix^3)` = 0
`B = mu_0/(4pi) vecm/x^3 = mu_0/(4pi) (vecm hatk)/x^3`
`int vecB.vec(dl) = int_R^a (- mu_0 vecmhatk)/(4pix^3) * vec(dl)`
∵ Angle between dl and m is 90°
So `int vecB.vec(dl) = int_R^a (- mu_0 |vecm| dl cos 90^circ)/(4pix^3)` = 0
(iv) Ampere's law along the quarter circle of radius 'a' and centre at the origin in the quadrant X-z plane as in figure here as on part (ii).
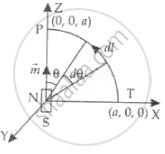
`int B.dl = int_(pi/2)^0 mu_0/(4pi) (vecm sin theta)/a^3 * ad theta`
`int B.dl = (mu_0vecm)/(4pia^2) [- cos theta]_(pi/2)^0`
θ = angle from axial line of dipole
`int B.dl = (mu_0vecm)/(4pia) [- cos theta + cos pi/2] = (mu_0vecm)/(4pia^2) (-1 + 0) = (-mu_0vecm)/(4pia^2)`
∴ Applying Ampere's law along close path starting from P to Q, Q to S and S to P.
`oint_(PQST) B.dl = int_P^Q vecB. vec(dl) + int_Q^S vecB.vec(dl) + int_S^T vecB. vec(dl) + int_T^P B.dl`
From parts (i), (ii), (iii) and (iv) substituting the values
`oint_(PQST) B.dl = (mu_0vecm)/(4pi) (1/a^2 - 1/R^2) + (mu_0vecm)/(4piR^2) + 0 + (-mu_0vecm)/(4pia^2)`
= `(mu_0vecm)/(4pia^2) - (mu_0vecm)/(4piR^2) + (mu_0vecm)/(4piR) - (mu_0vecm)/(4pia^2)`
`oint_(PQST) B.dl` = 0
This proves that Ampere's law is magnetism.
APPEARS IN
संबंधित प्रश्न
Two bar magnets are placed close to each other with their opposite poles facing each other. In absence of other forces, the magnets are pulled towards each other and their kinetic energy increases. Does it contradict our earlier knowledge that magnetic forces cannot do any work and hence cannot increase kinetic energy of a system?
Answer the following question in brief.
What happens if a bar magnet is cut into two pieces transverse to its length/along its length?
A closely wound solenoid of 800 turns and area of cross-section 2.5 × 10–4 m2 carries a current of 3.0 A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment?
A closely wound solenoid of 2000 turns and area of cross-section 1.6 × 10–4 m2, carrying a current of 4.0 A, is suspended through its centre allowing it to turn in a horizontal plane.
- What is the magnetic moment associated with the solenoid?
- What is the force and torque on the solenoid if a uniform horizontal magnetic field of 7.5 × 10–2 T is set up at an angle of 30° with the axis of the solenoid?
Which of the following statements about bar magnet is correct?
When current is double deflection is also doubled in
A magnetic needle suspended freely orients itself:-
Magnetic dipole moment is a ______
A proton has spin and magnetic moment just like an electron. Why then its effect is neglected in magnetism of materials?
There are two current carrying planar coils made each from identical wires of length L. C1 is circular (radius R) and C2 is square (side a). They are so constructed that they have same frequency of oscillation when they are placed in the same uniform B and carry the same current. Find a in terms of R.
