Advertisements
Advertisements
प्रश्न
Volume of a cylinder of height 3 cm is a 48π. Radius of the cylinder is ______.
विकल्प
48 cm
16 cm
4 cm
24 cm
उत्तर
Volume of a cylinder of height 3 cm is a 48π. Radius of the cylinder is 4 cm.
Explanation:
Given Height of cylinder h = 3 cm
Volume of cylinder V = 48π
Let Radius of cylincier = r
V = πr2h
48π = πr2 × 3
r2 = `48/3`
= 16
r = `sqrt(16)`
= 4 cm
APPEARS IN
संबंधित प्रश्न
Water flows, at 9 km per hour, through a cylindrical pipe of cross-sectional area 25 cm2. If this water is collected into a rectangular cistern of imensions 7.5 m by 5 m by 4 m; calculate therise in level in the cistern in 1 hour 15 minutes.

Calculate:
(a) the total surface area,
(b) the total volume of the solid and
(c) the density of the material if its total weight is 1.7 kg..
An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground is 85 m and height of the cylindrical part of 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for fold and for stitching. Give your answer to the nearest m2.
A metal pipe has a bore (inner diameter) of 5 cm. The pipe is 5 mm thick all round. Find the weight, in kilogram, of 2 metres of the pipe if 1 cm3 of the metal weights 7.7 g.
3080 cm3 of water is required to fill a cylindrical vessel completely and 2310 cm3 of water is required to fill it upto 5 cm below the top. Find :
- radius of the vessel.
- height of the vessel.
- wetted surface area of the vessel when it is half-filled with water.
The difference between the outer curved surface area and the inner curved surface area of a hollow cylinder is 352 cm2. If its height is 28 cm and the volume of material in it is 704 cm3; find its external curved surface area.
Water flows through a cylindrical pipe of internal diameter 7 cm at 36 km/hr. Calculate the time in minutes it would take to fill the cylindrical tank, the radius of whose base is 35 cm, and height is 1 m.
The volume of the largest right circular cone that can be fitted in a cube whose edge is 2r equals to the volume of a hemisphere of radius r.
The water for a factory is stored in a hemispherical tank whose internal diameter is 14 m. The tank contains 50 kilolitres of water. Water is pumped into the tank to fill to its capacity. Calculate the volume of water pumped into the tank.
Radius of a cylinder is r and the height is h. Find the change in the volume if the height remains same and the radius is halved.
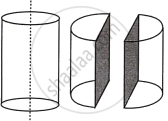
A solid metallic cylinder is cut into two identical halves along its height (as shown in the diagram). The diameter of the cylinder is 7 cm and the height is 10 cm.
Find:
- The total surface area (both the halves).
- The total cost of painting the two halves at the rate of ₹ 30 per cm2 `("Use" π = 22/7)`.