Advertisements
Advertisements
प्रश्न
Water flows through a horizontal tube as shown in figure. If the difference of heights of water column in the vertical tubes is 2 cm, and the areas of cross section at A and B are 4 cm2 and 2 cm2 respectively, find the rate of flow of water across any section.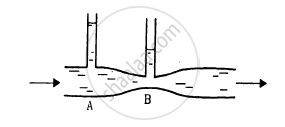
उत्तर
Given:
Difference in the heights of water columns in vertical tubes = 2 cm
Area of cross section at A, aA = 4 cm2
Area of cross section at B, aB = 2 cm2
Now, let vA and vB be the speeds of water at A and B, respectively.
From the equation of continuity, we have:
\[v_A a_A = v_B \times a_B \]
\[ \Rightarrow v_A \times 4 = v_B \times 2\]
\[ \Rightarrow v_B = 2 v_A . . . (i)\]
From Bernoulli's equation, we have:
\[\frac{1}{2}\rho v_A^2 + ρg h_A + p_A = \frac{1}{2}\rho v_B^2 +ρg h_B + p_B \]
\[ \Rightarrow \frac{1}{2}\rho v_A^2 + p_A = \frac{1}{2}\rho v_B^2 + p_B \]
\[ \Rightarrow p_A - p_B = \frac{1}{2}\rho\left( v_B^2 - v_A^2 \right)\]
Here,
pA and pB are the pressures at A and B, respectively.
hA and hB are the heights of water columns at point A and B, respectively.
ρ is the density of the liquid.
Thus, we have:
\[\frac{1}{2} \times 1 \times \left( 4 v_A^2 - v_A^2 \right)\]
\[ \Rightarrow 2 \times 1 \times 1000 = \frac{1}{2} \times 1 \times 3 v_A^2 \]
\[[ p_A - p_B = 2 cm = 2 \times 1 \times 1000 {\text{ dyne }/ {\text{cm}}^2} (\text{water column})]\]
\[ \Rightarrow v_A^2 = \sqrt{\frac{4000}{3}} = 36 . 51 cm/s\]
\[ \therefore\text{ Rate of flow }= v_A a_A = 36 . 51 \times 4\]
\[ = 146 {\text{ cm}}^3 /s\]
Hence, the required rate of flow of water across any section is 146 cm3/s.
APPEARS IN
संबंधित प्रश्न
While watering a distant plant, a gardener partially closes the exit hole of the pipe by putting his finger on it. Explain why this results in the water stream going to a larger distance.
At Deoprayag (Garwal, UP) river Alaknande mixes with the river Bhagirathi and becomes river Ganga. Suppose Alaknanda has a width of 12 m, Bhagirathi has a width of 8 m and Ganga has a width of 16 m. Assume that the depth of water is same in the three rivers, Let the average speed of water in Alaknanda be 20 km/h and in Bhagirathi be 16 km/h. Find the average speed of water in the river Ganga.
Water flows through a tube shown in figure. The area of cross section at A and B are 1 cm2 and 0.5 cm2 respectively. The height difference between A and B is 5 cm. If the speed of water at A is 10 cm s find (a) the speed at B and (b) the difference in pressures at A and B.

Water flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5 cm2 and 2 cm2 respectively. The rate of flow of water through the tube is 500 cm3 s−1. Find the difference of mercury levels in the U-tube.
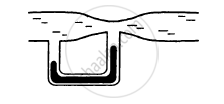
A vessel completely filled with water has holes 'A' and 'B' at depths 'h' and '3h' from the top respectively. Hole 'A' is a square of side 'L' and 'B' is a circle of radius 'r'. The water flows out per second from both the holes in the same. Then 'L' is equal to ______.
An ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5 cm and 3.75 cm. The ratio of the velocities in the two pipes is ______.
Explain the continuity condition for a flow tube. Show that the flow speed is inversely proportional to the cross-sectional area of a flow tube.
