Advertisements
Advertisements
प्रश्न
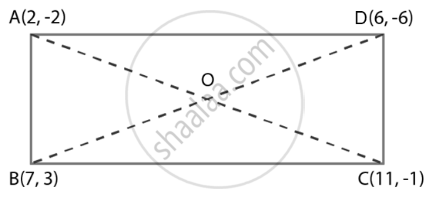
What type of a quadrilateral do the points A(2, –2), B(7, 3), C(11, –1) and D(6, –6) taken in that order, form?
उत्तर
The points are A(2, –2), B(7, 3), C(11, –1) and D(6, –6)
Using distance formula,
d = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
AB = `sqrt((7 - 2)^2 + (3 + 2)^2`
= `sqrt((5)^2 + (5)^2`
= `sqrt(25 + 25)`
= `sqrt(50)`
= 5`sqrt(2)`
BC = `sqrt((11 - 7)^2 + (-1 - 3)^2`
= `sqrt((4)^2 + (-4)^2`
= `sqrt(16 + 16)`
= `sqrt(32)`
= `4sqrt(2)`
CD = `sqrt((6 - 11)^2 + (-6 + 1)^2`
= `sqrt((-5)^2 + (-5)^2`
= `sqrt(25 + 25)`
= `sqrt(50)`
= `5sqrt(2)`
DA = `sqrt((2 - 6)^2 + (-2 + 6)^2`
= `sqrt((-4)^2 + (4)^2`
= `sqrt(16 + 16)`
= `sqrt(32)`
= `4sqrt(2)`
Finding diagonals AC and BD, we get,
AC = `sqrt((11 - 2)^2 + (-1 + 2)^2`
= `sqrt((9)^2 + (1)^2`
= `sqrt(81 + 1)`
= `sqrt(82)`
And BD = `sqrt((6 - 7)^2 + (-6 - 3)^2`
= `sqrt((-1)^2 + (-9)^2`
= `sqrt(1 + 81)`
= `sqrt(82)`
The quadrilateral formed is rectangle.
APPEARS IN
संबंधित प्रश्न
Find the distance of a point P(x, y) from the origin.
ABC is a triangle and G(4, 3) is the centroid of the triangle. If A = (1, 3), B = (4, b) and C = (a, 1), find ‘a’ and ‘b’. Find the length of side BC.
Find the distance between the following pair of points:
(asinα, −bcosα) and (−acos α, bsin α)
Find the distance between the following pairs of point in the coordinate plane :
(13 , 7) and (4 , -5)
P and Q are two points lying on the x - axis and the y-axis respectively . Find the coordinates of P and Q if the difference between the abscissa of P and the ordinates of Q is 1 and PQ is 5 units.
From the given number line, find d(A, B):

In what ratio does the point P(−4, y) divides the line segment joining the points A(−6, 10) and B(3, −8)? Hence find the value of y.
Show that (-3, 2), (-5, -5), (2, -3) and (4, 4) are the vertices of a rhombus.
Find the distance of the following points from origin.
(5, 6)
If the distance between the points (4, P) and (1, 0) is 5, then the value of p is ______.
