Advertisements
Advertisements
प्रश्न
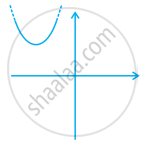
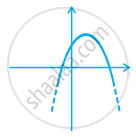
Which of the following is not the graph of a quadratic polynomial?
विकल्प
उत्तर
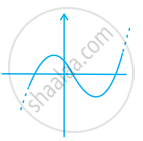
Explanation:
For any quadratic polynomial ax2 + bx + c, a ≠ 0
The graph of the corresponding equation y = ax2 + bx + c has one of the two shapes either open upwards like ∪ or open downwards like ∩ depending on whether a > 0 or a < 0. These curves are called parabolas.
So, option (d) cannot be possible.
Also, the curve of a quadratic polynomial crosses the X-axis on at most two points but in option (d) the curve crosses the X-axis on the three points, so it does not represent the quadratic polynomial.
APPEARS IN
संबंधित प्रश्न
One zero of the polynomial `3x^3+16x^2 +15x-18 is 2/3` . Find the other zeros of the polynomial.
Write the zeros of the polynomial `f(x) = x^2 – x – 6`.
If 𝛼, 𝛽 are the zeroes of the polynomial `f(x) = x^2 – 5x + k` such that 𝛼 - 𝛽 = 1, find the value of k = ?
If the zeroes of the polynomial `f(x) = x^3 – 3x^2 + x + 1` are (a – b), a and (a + b), find the values of a and b.
The zeroes of the quadratic polynomial x2 + 99x + 127 are ______.
If one of the zeroes of the quadratic polynomial (k -1)x² + kx + 1 the value of k is ______.
If α and β are the zeroes of the polynomial x2 – 1, then the value of (α + β) is ______.
The zeroes of the polynomial 3x2 + 11x – 4 are ______.
The zeroes of the quadratic polynomial 16x2 – 9 are ______.
If α and β are the zeroes of the polynomial x2 + x − 2, then find the value of `alpha/beta+beta/alpha`