Question

Write an equation of a line passing through the point representing solution of the pair of linear equations x + y = 2 and 2x – y = 1. How many such lines can we find?

Answer 1

Given pair of linear equation are

x + y – 2 = 0   ......(i)

And 2x – y – 1 = 0   ......(ii)

On comparing with ax + by + c = 0, we get

a₁ = 1, b₁ = 1 and c₁ = –2 ......[From (i)]

a₂ = 2, b₂ = –1 and c₂ = –1 .....[From (ii)]

Here, `a_1/a_2 = 1/2`,

`b_1/b_2 = 1/(-1)`

And `c_1/c_2 = (-2)/(-1) = 2/1`

⇒ `a_1/a_2 ≠ b_1/b_2`

So, both lines intersect at a point.

Therefore, the pair of equations has a unique solution.

Hence, these equations are consistent.

Now, x + y = 2

⇒ y = 2 – x

x	0	2	1
y	2	0	1

And 2x – y – 1 = 0

⇒ y = 2x – 1

x	0	`1/2`	1
y	–1	0	1

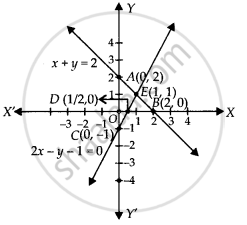
The given lines intersect at E(1, 1).

Hence, infinite lines can pass through the intersection point of linear equations x + y = 2 and 2x – y = 1

i.e., E(1, 1) like as y = x, 2x + y = 3, x + 2y = 3 so on.