Advertisements
Advertisements
प्रश्न
Write the following equation in the form ax2 + bx + c= 0, then write the values of a, b, c for the equation.
3m2 = 2m2 – 9
उत्तर
3m2 = 2m2 – 9
\[\Rightarrow 3 m^2 - 2 m^2 + 9 = 0\]
\[ \Rightarrow m^2 + 0m + 9 = 0\]
So, it is of the form ax2 + bx + c = 0 where a = 1, b = 0 and c = 9.
APPEARS IN
संबंधित प्रश्न
The divisor and quotient of the number 6123 are same and the remainder is half the divisor. Find the divisor.
If the roots of` 5x^2-k+1=0` are real and distinct then
(a)`-2sqrt5<k2<sqrt5` (b)` k>2sqrt5 ` only
(c)` k<-2sqrt5` (d) either `k>2sqrt5 or k<-2sqrt5`
If the equation `x^2-5x+1=0` has no real roots then
(a)`k<-2`
(b)`k>2`
(c) `-2<k<2`
(d) None of these
The perimeter of a rectangle is 82m and its area is `400m^2` . The breadth of the rectangle is
(a) 25m (b)20m
(c) 16m (d)9m
If `x=-1/2` is a solution of the quadratic equation `3x^2+2kx-3=0`
Find the value of k.
Find the roots of the quadratic equation `2x^2-x-6=0`
If 1 is a root of the equation `ay^2+ay+3=0` and `y^2+y+b=0` then find the value of ab.
Solve `x^2+5x-(a^2+a-6)=0`
Decide whether the following equation is quadratic equation or not.
(m + 2) (m – 5) = 0
If 460 is divided by a natural number, quotient is 6 more than five times the divisor and remainder is 1. Find quotient and divisor.
Which one is the quadratic equation?
Solve the following quadratic equation.
5m2 + 2m + 1 = 0
Find the value of m so that the quadratic equation mx (x − 7) + 49 = 0 has two equal roots.
Which of the following is a quadratic equation ?
Solve any two of the following.
Solve : `3x+y=14 ; x-y=2`
Find k, one of the roots of the quadratic equation kx2 - 7x + 12 = 0 is 3.
Complete the following activity to form a quadratic equation.
Activity:
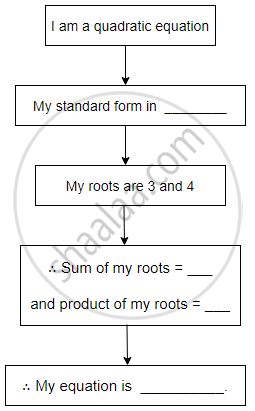
Form a quadratic equation such that one of its roots is 5. Form a quadratic equation for it and write. (For the formation of word problems you can use quantities like age, rupees, or natural numbers.) (Sample solution for the above example is given below students can take another number to form another example)
Solution:
We need one of the solutions of the quadratic equation as 5.
Then we can take another root as any number like a positive or negative number or zero. Here I am taking another root of the quadratic equation as 2.
Then we can form a word problem as below,
Smita is younger than her sister Mita by 3 years (5 – 2 = 3). If the product of their ages is (5 × 2 = 10). Then find their present ages.
Let the age of Mita be x.
Therefore age of Smita = x – 3
By the given condition,
x(x – 3) = 10
x2 – 3x – 10 = 0
The ratio of fruit trees and vegetable trees in an orchard is 3:4. If 6 more trees of each type are planted, the ratio of trees would be 6:7. Find the number of fruit trees and vegetable trees in the orchard.
The ratio of fruit trees and vegetable trees = 3:4
So, let the number of fruit trees= 3x and the number of vegetable trees = `square`
From the given condition,
`(3x + square)/(square + square) = square/square`
`square (3x + square) = square (square + square)`
`square + square = square + square`
`square - square = square - square`
`- square = - square`
`square = square`
x = `square`
∴ Number of fruit trees in the orchard = 3x = 3 × `square` = `square` and number of vegetable trees in the orchard = 4x = 4 × `square` = `square`
Hence, the number of fruit trees and vegetable trees in the orchard are `square` and `square` respectively.
A tank can be filled up by two taps in 6 hours. The smaller tap alone takes 5 hours more than the bigger tap alone. Find the time required by each tap to fill the tank separately.
