Advertisements
Advertisements
प्रश्न
यदि AB = 12 cm, BC = 16 cm और AB रेखाखंड BC पर लंब है, तो A, B और C से होकर जाने वाले वृत्त की त्रिज्या है
विकल्प
6 cm
8 cm
10 cm
12 cm
उत्तर
10 cm
स्पष्टीकरण -
प्रश्न में दिया गया है, AB = 12 सेमी और BC = 16 सेमी।
एक वृत्त में, BC ⊥ AB, इसलिए, इसका अर्थ है कि AC वृत्त का व्यास होगा।
अब, समकोण त्रिभुज ABC में पाइथागोरस प्रमेय का उपयोग करके।
AC2 = AB2 + BC2
AC2 = (12)2 + (16)2
AC2 = 144 + 256
AC2 = 400
AC = 20 सेंमी
इसलिए, वृत्त की त्रिज्या = `1/2 xx AC`
= `1/2 xx 20`
= 10 सेमी
अतः वृत्त की त्रिज्या 10 सेमी है।
APPEARS IN
संबंधित प्रश्न
एक चाप _______ होता है, जब इसके सिरे एक व्यास के सिरे हों।
एक वृत्त, जिस तल पर स्थित है, उसे _______ भागों में विभाजित करता है।
वृत्त एक समतल आकृति है।
संलग्न आकृति देखकर लिखिए:
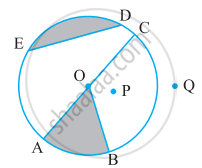
वृत का केंद्र
संलग्न आकृति देखकर लिखिए:
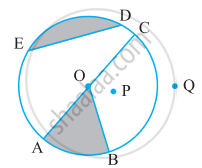
तीन त्रिज्याएँ
क्या वृत का प्रत्येक व्यास उसकी एक जीवा भी होता है?
सत्य या असत्य बताइए:
वृत का केंद्र सदैव उसके अभ्यंतर में स्थित होता है।
किसी वृत्त का AD एक व्यास है और AB एक जीवा है। यदि AD = 34 cm, AB = 30 cm है, तो वृत्त के केंद्र से AB की दूरी है
आकृति में O एक वृत्त का केंद्र है। वृत्त की सभी जीवाओं के नाम लिखिए।
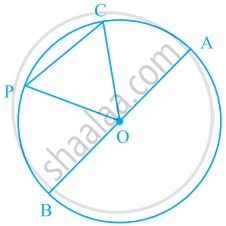
आकृति में O एक वृत्त का केंद्र है। त्रिज्याखंड OAC और OPB को छायांकित'कीजिए।