Advertisements
Advertisements
Question
यदि AB = 12 cm, BC = 16 cm और AB रेखाखंड BC पर लंब है, तो A, B और C से होकर जाने वाले वृत्त की त्रिज्या है
Options
6 cm
8 cm
10 cm
12 cm
Solution
10 cm
स्पष्टीकरण -
प्रश्न में दिया गया है, AB = 12 सेमी और BC = 16 सेमी।
एक वृत्त में, BC ⊥ AB, इसलिए, इसका अर्थ है कि AC वृत्त का व्यास होगा।
अब, समकोण त्रिभुज ABC में पाइथागोरस प्रमेय का उपयोग करके।
AC2 = AB2 + BC2
AC2 = (12)2 + (16)2
AC2 = 144 + 256
AC2 = 400
AC = 20 सेंमी
इसलिए, वृत्त की त्रिज्या = `1/2 xx AC`
= `1/2 xx 20`
= 10 सेमी
अतः वृत्त की त्रिज्या 10 सेमी है।
APPEARS IN
RELATED QUESTIONS
यदि एक वृत्त को तीन बराबर चापों में बाँट दिया जाए, तो प्रत्येक भाग दीर्घ चाप होता है।
संलग्न आकृति देखकर लिखिए:
वृत का केंद्र
संलग्न आकृति देखकर लिखिए:

एक व्यास
क्या वृत का प्रत्येक व्यास उसकी एक जीवा भी होता है?
सत्य या असत्य बताइए:
वृत का केंद्र सदैव उसके अभ्यंतर में स्थित होता है।
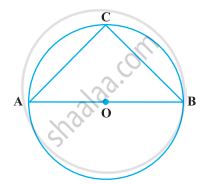
निम्नलिखित आकृति में, यदि AOB वृत्त का एक व्यास तथा AC = BC है, तो ∠CAB बराबर है
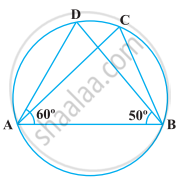
निम्नलिखित आकृति में, यदि ∠DAB = 60°, ∠ABD = 50° है, तो ∠ACB बराबर है
दो बिंदुओं A और B से होकर 3 cm त्रिज्या का एक वृत्त खींचा जा सकता है, यदि AB = 6 cm है।
एक वृत्त की त्रिज्या `sqrt2` cm है। 2 cm लंबाई वाली जीवा द्वारा यह वृत्त दो वृत्त-खंडों में विभाजित किया जाता है। सिद्ध कीजिए कि इस जीवा द्वारा दीर्घ वृत्त-खंड के किसी बिंदु पर बना कोण 45° है।
चाँदे का प्रयोग किए बिना, दो न्यूनकोण और एक अधिक कोण खींचिए। इन कोणों की मापों का आकलन कीजिए। इनको चाँदे से मापिए और देखिए कि आपका आकलन कितना सही है।
