Advertisements
Advertisements
Question
निम्नलिखित आकृति में, यदि OA = 5 cm, AB = 8 cm तथा OD जीवा AB पर लंब है, तो CD बराबर है
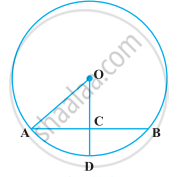
Options
2 cm
3 cm
4 cm
5 cm
Solution
2 cm
स्पष्टीकरण -

हम जानते हैं कि, वृत्त के केंद्र से जीवा पर डाला गया लंब जीवा को समद्विभाजित करता है।
AC = CB = `1/2` AB = `1/2` × 8 = 4 cm
दिया गया है OA = 5 cm
AO2 = AC2 + OC2
(5)2 = (4)2 + OC2
25 = 16 + OC2
OC2 = 25 – 16 = 9
OC = 3 cm ...[सकारात्मक वर्गमूल लेने पर, क्योंकि लंबाई हमेशा धनात्मक होती है।]
OA = OD ...[एक वृत्त की समान त्रिज्या]
OD = 5 cm
CD = OD – OC
= 5 – 3
= 2 cm
APPEARS IN
RELATED QUESTIONS
यदि एक वृत्त को तीन बराबर चापों में बाँट दिया जाए, तो प्रत्येक भाग दीर्घ चाप होता है।
त्रिज्यखंड, जीवा एवं संगत चाप के बीच का क्षेत्र होता है।
सत्य या असत्य बताइए:
वृत के दो व्यास अवश्य ही प्रतिच्छेद करेंगे।
किसी वृत्त का AD एक व्यास है और AB एक जीवा है। यदि AD = 34 cm, AB = 30 cm है, तो वृत्त के केंद्र से AB की दूरी है
निम्नलिखित आकृति में, BC वृत्त का व्यास है तथा ∠BAO = 60° है। तब, ∠ADC बराबर है
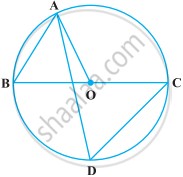
निम्नलिखित आकृति में, ∠AOB = 90° और ∠ABC = 30° है। तब, ∠CAO बराबर है :
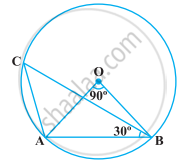
एक वृत्त की दो जीवाएँ AB और AC उसके केंद्र पर क्रमश : 90° और 150° के कोण अंतरित करती हैं। ∠BAC ज्ञात कीजिए, यदि AB और AC केंद्र के विपरीत ओर स्थित हैं।
त्रिभुज के तीनों कोणों के समद्विभाजक संगामी होते हैं। उनके संगामी बिंदु को क्या कहते हैं?
2.9 सेमी त्रिज्यावाले वृत्त की सबसे बड़ी जीवा की लंबाई कितनी हो सकती है?
किसी O केंद्रवाले वृत्त की त्रिज्या 4 सेमी है। l(OP) = 4.2 सेमी हो तो बिंदु ‘P’ कहाँ होगा?
