Advertisements
Advertisements
Question
एक वृत्त की दो जीवाएँ AB और AC उसके केंद्र पर क्रमश : 90° और 150° के कोण अंतरित करती हैं। ∠BAC ज्ञात कीजिए, यदि AB और AC केंद्र के विपरीत ओर स्थित हैं।
Solution
त्रिभुज BOA में,
OB = OA ...[दोनों वृत्त की त्रिज्या हैं।]
∠OAB = ∠OBA ...(i) [समान भुजाओं के सम्मुख कोण बराबर होते हैं।]

अब, त्रिभुज OAB में,
∠OBA + ∠AOB + ∠AOC = 180° ...[त्रिभुज के कोण योग गुण द्वारा]
∠OAB + ∠OAB + 90° = 180° ...[समीकरण (i) से]
2∠OAB = 180° – 90°
2∠OAB = 90°
∠OAB = 45°
पुनः, त्रिभुज AOC में,
AO = OC ...[त्रिज्या या वृत्त]
∠OCA = ∠OAC ...(ii) [समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
अब, त्रिभुज के कोण गुण योग द्वारा,
∠AOC + ∠OAC + ∠OCA = 180°
150° + 2∠OAC = 180° ...[समीकरण (ii) से]
2∠OAC = 180° – 150°
2∠OAC = 30°
∠OAC = 15°
∠BAC = ∠OAB + ∠OAC = 45° + 15° = 60°
APPEARS IN
RELATED QUESTIONS
एक वृत्त, जिस तल पर स्थित है, उसे _______ भागों में विभाजित करता है।
संलग्न आकृति देखकर लिखिए:
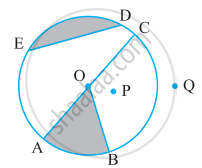
बहिर्भाग में एक बिंदु
संलग्न आकृति देखकर लिखिए:
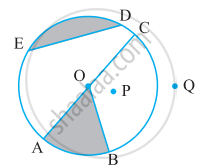
एक त्रिज्यखंड
सत्य या असत्य बताइए:
वृत के दो व्यास अवश्य ही प्रतिच्छेद करेंगे।
सत्य या असत्य बताइए:
वृत का केंद्र सदैव उसके अभ्यंतर में स्थित होता है।
यदि AB = 12 cm, BC = 16 cm और AB रेखाखंड BC पर लंब है, तो A, B और C से होकर जाने वाले वृत्त की त्रिज्या है
एक वृत की दो जीवाएँ AB और CD में से प्रत्येक केंद्र से 4 cm की दूरी पर है। तब, AB = CD है।
दो बिंदुओं A और B से होकर 3 cm त्रिज्या का एक वृत्त खींचा जा सकता है, यदि AB = 6 cm है।
निम्नलिखित आकृति में, ∠ACB = 40° है। ∠OAB ज्ञात कीजिए।
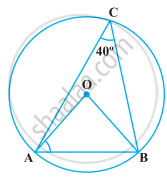
किसी O केंद्रवाले वृत्त की त्रिज्या 4 सेमी है। l(OP) = 4.2 सेमी हो तो बिंदु ‘P’ कहाँ होगा?
