Advertisements
Advertisements
Question
किसी वृत्त का AD एक व्यास है और AB एक जीवा है। यदि AD = 34 cm, AB = 30 cm है, तो वृत्त के केंद्र से AB की दूरी है
Options
17 cm
15 cm
4 cm
8 cm
Solution
8 cm
स्पष्टीकरण -
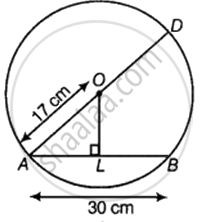
दिया गया है - वृत्त का व्यास = d = AD = 34 cm
∴ वृत्त की त्रिज्या = r = `d/2` = AO = 17 cm
जीवा AB की लम्बाई = 30 cm
चूँकि एक जीवा को समद्विभाजित करने के लिए एक वृत्त के केंद्र के माध्यम से खींची गई रेखा जीवा के लंबवत होती है, AOL एक समकोण त्रिभुज है जिसमें L, AB का द्विभाजक है।
∴ AL = `1/2`(AB) = 15 cm
समकोण त्रिभुज AOB में, पाइथागोरस प्रमेय द्वारा, हमारे पास,
(AO)2 = (OL)2 + (AL)2
⇒ (17)2 = (OL)2 + (15)2
⇒ (OL)2 = (17)2 – (15)2
⇒ (OL)2 = 289 – 225
⇒ (OL)2 = 64
दोनों पक्षों का वर्गमूल निकालें,
⇒ (OL) = 8
∴ वृत्त के केंद्र से AB की दूरी 8 सेमी है।
APPEARS IN
RELATED QUESTIONS
वृत्त का केन्द्र वृत्त के ______ में स्थित है।
वृत्त एक समतल आकृति है।
संलग्न आकृति देखकर लिखिए:

एक व्यास
संलग्न आकृति देखकर लिखिए:
बहिर्भाग में एक बिंदु
क्या वृत का प्रत्येक जीवा उसका एक व्यास भी होती है?
कोई वृत खींचिए और निम्न को अंकित कीजिए:
-
उसका केंद्र
-
एक वृतखंड
-
एक त्रिज्या
-
उसके अभ्यंतर में एक बिंदु
-
एक व्यास
-
उसके बहिर्भाग में एक बिंदु
-
एक त्रिज्यखंड
- एक चाप
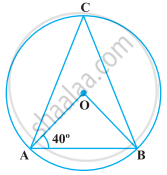
निम्नलिखित आकृति में, यदि ∠OAB = 40° है, तो ∠ACB बराबर है
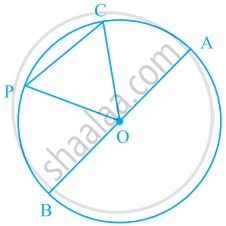
आकृति में O एक वृत्त का केंद्र है। वृत्त की सभी जीवाओं के नाम लिखिए।
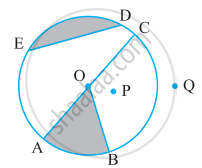
आकृति में O एक वृत्त का केंद्र है। त्रिज्याखंड OAC और OPB को छायांकित'कीजिए।
किसी वृत्त की समांतर जीवाओं की लंबाई क्रमशः 6 सेमी तथा 8 सेमी है। उस वृत्त की त्रिज्या 5 सेमी हो तो उन जीवाओं के बीच दूरी कितनी होगी?
