Advertisements
Advertisements
प्रश्न
किसी वृत्त का AD एक व्यास है और AB एक जीवा है। यदि AD = 34 cm, AB = 30 cm है, तो वृत्त के केंद्र से AB की दूरी है
पर्याय
17 cm
15 cm
4 cm
8 cm
उत्तर
8 cm
स्पष्टीकरण -
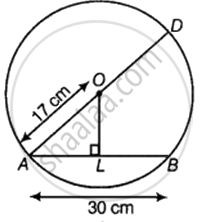
दिया गया है - वृत्त का व्यास = d = AD = 34 cm
∴ वृत्त की त्रिज्या = r = `d/2` = AO = 17 cm
जीवा AB की लम्बाई = 30 cm
चूँकि एक जीवा को समद्विभाजित करने के लिए एक वृत्त के केंद्र के माध्यम से खींची गई रेखा जीवा के लंबवत होती है, AOL एक समकोण त्रिभुज है जिसमें L, AB का द्विभाजक है।
∴ AL = `1/2`(AB) = 15 cm
समकोण त्रिभुज AOB में, पाइथागोरस प्रमेय द्वारा, हमारे पास,
(AO)2 = (OL)2 + (AL)2
⇒ (17)2 = (OL)2 + (15)2
⇒ (OL)2 = (17)2 – (15)2
⇒ (OL)2 = 289 – 225
⇒ (OL)2 = 64
दोनों पक्षों का वर्गमूल निकालें,
⇒ (OL) = 8
∴ वृत्त के केंद्र से AB की दूरी 8 सेमी है।
APPEARS IN
संबंधित प्रश्न
एक चाप _______ होता है, जब इसके सिरे एक व्यास के सिरे हों।
संलग्न आकृति देखकर लिखिए:
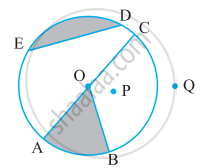
अभ्यंतर में दो बिंदु
संलग्न आकृति देखकर लिखिए:
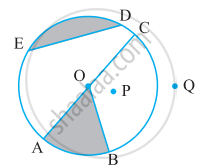
एक त्रिज्यखंड
क्या वृत का प्रत्येक जीवा उसका एक व्यास भी होती है?
सत्य या असत्य बताइए:
वृत के दो व्यास अवश्य ही प्रतिच्छेद करेंगे।
ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इस चतुर्भुज के परिगत वृत्त का एक व्यास है तथा ∠ADC = 140° है। तब, ∠BAC बराबर है
निम्नलिखित आकृति में, BC वृत्त का व्यास है तथा ∠BAO = 60° है। तब, ∠ADC बराबर है
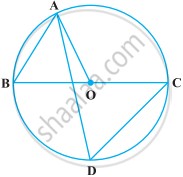
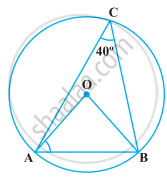
निम्नलिखित आकृति में, ∠ACB = 40° है। ∠OAB ज्ञात कीजिए।
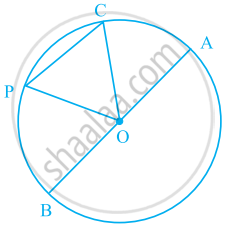
आकृति में O एक वृत्त का केंद्र है। वृत्त की सभी त्रिज्याओं के नाम लिखिए।
त्रिभुज के सभी शीर्षबिंदुओं से जाने वाले वृत्त को क्या कहते हैं?
