Advertisements
Advertisements
प्रश्न
यदि दो रेखाएँ प्रतिच्छेद करती हैं तो सिद्ध कीजिए कि शीर्षाभिमुख कोण बराबर होते हैं।
उत्तर
आइए आकृति बनाते हैं।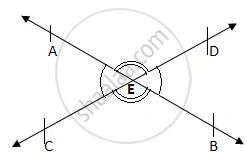
यहाँ, हम यह देख सकते हैं।
AB और CD एक दूसरे को बिंदु E पर काटते हैं।
शीर्षाभिमुख कोणों के दो युग्म हैं -
पहला युग्म - ∠AEC और ∠BED
दूसरा युग्म - ∠AED और ∠BEC
हमें सिद्ध करना है कि शीर्षाभिमुख कोण बराबर होते हैं, अर्थात,
∠AEC = ∠BED और ∠AED = ∠BEC
अब, हम देख सकते हैं कि किरण AE रेखा CD पर लंब है।
हम जानते हैं कि, यदि एक किरण एक रेखा पर खड़ी हो, तो आसन्न कोणों का योग 180° के बराबर होता है।
⇒ ∠AEC + ∠AED = 180° (रैखिक युग्म अभिगृहीत द्वारा) ...(i)
इसी प्रकार, किरण DE रेखा AEB पर खड़ी है।
⇒ ∠AED + ∠BED = 180° (रैखिक युग्म अभिगृहीत द्वारा) ...(ii)
समीकरण (i) और (ii) से, हमारे पास है
∠AEC + ∠AED = ∠AED + ∠BED
⇒ ∠AEC = ∠BED ...(iii)
इसी प्रकार, किरण BE रेखा CED पर खड़ी है।
⇒ ∠DEB + ∠CEB = 180° (रैखिक युग्म अभिगृहीत द्वारा) ...(iv)
साथ ही, किरण CE, रेखा AEB के लंबवत है।
⇒ ∠CEB + ∠AEC = 180° (रैखिक युग्म अभिगृहीत द्वारा) ...(v)
समीकरण (iv) और (v) से, हमारे पास है।
∠DEB + ∠CEB = ∠CEB + ∠AEC
⇒ ∠DEB = ∠AEC ...(vi)
इस प्रकार, समीकरण (iii) और समीकरण (vi) से, हमारे पास है।
∠AEC = ∠BED और ∠DEB = ∠AEC
इसलिए, यह सिद्ध होता है कि शीर्षाभिमुख कोण बराबर होते हैं।