Advertisements
Advertisements
प्रश्न
∆ABC के अंतःकोण ∠B और बहिष्कोण ∠ACD के समद्विभाजक बिंदु T पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि `∠BTC = 1/2 ∠BAC` हैं।
उत्तर
∆ABC में दिया गया है, SC को D तक बढ़ाएँ और ∠ABC और ∠ACD के द्विभाजक बिंदु T पर मिलते हैं।
`∠BTC = 1/2 ∠BAC` साबित करने के लिए,
उपपत्ति - ∆ABC में, ∠C एक बाह्य कोण है।
∴ ∠ACD = ∠ABC + ∠CAB ...[त्रिभुज के बहिष्कोण का दो विपरीत कोणों के योग से]
⇒ `1/2 ∠ACD = 1/2 ∠CAB + 1/2 ∠ABC` ...[दोनों पक्षों को 2 से विभाजित करने पर]
⇒ `∠TCD = 1/2 ∠CAB + 1/2 ∠ABC` ...(i) `[∵ CT, ∠ACD "का समद्विभाजक है" ⇒ 1/2 ∠ACD = ∠TCD]`
∆BTC में, ∠TCD = ∠BTC + ∠CBT ...[त्रिभुज का बाह्य कोण दो विपरीत आंतरिक कोणों के योग के बराबर होता है।]
⇒ `∠TCD = ∠BTC + 1/2 ∠ABC` ...(ii) `[∵ ∠ABC "का" BT "समद्विभाजक" ⇒ ∠CBT = 1/2 ∠ABC]`
समीकरण (i) और (ii) से,
`1/2 ∠CAB + 1/2 ∠ABC = ∠BTC + 1/2 ∠ABC`
⇒ `∠BTC = 1/2 ∠CAB`
या `∠BTC = 1/2 ∠BAC`
APPEARS IN
संबंधित प्रश्न
यदि दो प्रतिच्छेदी रेखाओं से बना एक कोण समकोण है, तो अन्य तीन कोणों के बारे में आप क्या कह सकते हैं? अपने उत्तर का कारण दीजिए।
निम्नलिखित आकृति में, कौन-सी दो रेखाएँ समांतर हैं और क्यों?
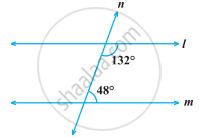 |
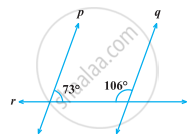 |
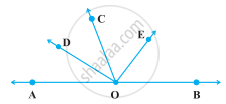
निम्नलिखित आकृति में, OD कोण ∠AOC का समद्विभाजक है, OE कोण ∠BOC का समद्विभाजक है तथा OD ⊥ OE है। दर्शाइए कि A, O और B सरेख हैं।
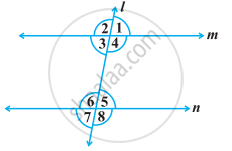
निम्नलिखित आकृति में, ∠1 = 60° और ∠6 = 120° है। दर्शाइए कि m और n समांतर हैं।
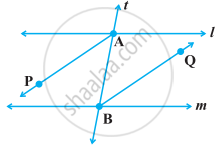
AP और BQ उन दो एकांतर अंतःकोणों के समद्विभाजक हैं जो समांतर रेखाओं l और m के तिर्यक रेखा t द्वारा प्रतिच्छेद से बनते हैं (आकृति)। दर्शाइए कि AP || BQ है।
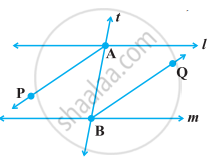
यदि निम्नलिखित आकृति में, एकांतर अंतःकोणों के समद्विभाजक AP और BQ समांतर हैं, तो दर्शाइए कि l ॥ m है।
एक त्रिभुज ABC का कोण A समकोण है। BC पर L एक बिंदु इस प्रकार है कि AL ⊥ BC है। सिद्ध कीजिए कि ∠BAL = ∠ACB है।
दो रेखाएँ क्रमश: दो समांतर रेखाओं पर लंब हैं। दर्शाइए कि ये दोनों रेखाएँ परस्पर समांतर हैं।
सिद्ध कीजिए कि एक दिए हुए बिंदु से होकर, हम एक दी हुई रेखा पर केवल एक लंब ही खींच सकते हैं।
[संकेत : विरोधाभास द्वारा उपपत्ति का प्रयोग कीजिए।]
