Advertisements
Advertisements
प्रश्न
यदि किसी बहुफलकी के 12 फलक और 20 शीर्ष हैं, तो इस ठोस में किनारों की संख्या ______ है।
उत्तर
यदि किसी बहुफलकी के 12 फलक और 20 शीर्ष हैं, तो इस ठोस में किनारों की संख्या 30 है।
स्पष्टीकरण -
हम जानते हैं कि, किसी भी बहुफलक के लिए यूलर का सूत्र F + V – E = 2 है।
दिया गया है, फलक, F = 12, शीर्ष, V = 20
अब, यूलर के सूत्र में F और V का मान रखने पर, हमें 12 + 20 – E = 2 प्राप्त होता है।
⇒ 32 – E = 2
⇒ 32 – 2 = E
⇒ E = 30
अतः, किनारों की संख्या = 30
APPEARS IN
संबंधित प्रश्न
क्या किसी बहुफलक के 10 फलक, 20 किनारे और 15 शीर्ष हो सकते है?
निम्न में से कौन एक सम बहुफलकी है?
निम्न में से कौन एक बहुफलकी के लिए सत्य नहीं हो सकता?
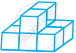 में घनों की संख्या ______ है।
में घनों की संख्या ______ है।
सम बहुफलकियों की कुल संख्या ______ है।
निम्न आकारों को देखिए और बताइए कि इनमें कौन-कौन बहुफलकी हैं।
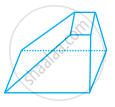
निम्न आकारों को देखिए और बताइए कि इनमें कौन-कौन बहुफलकी हैं।
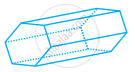
निम्न आकारों को देखिए और बताइए कि इनमें कौन-कौन बहुफलकी हैं।

क्या किसी बहुफलकी में V = F = 9 और E = 16 हो सकता है? यदि हाँ, तो इसकी आकृति खींचिए।
एक बहुफलकी में 40 फलक और 60 किनारे हैं। इस ठोस के शीषों की संख्या ज्ञात कीजिए।
