Advertisements
Advertisements
प्रश्न
यूक्लिडीय ज्यामिति केवल वक्र पृष्ठों के लिए ही मान्य है।
विकल्प
सत्य
असत्य
उत्तर
यह कथन असत्य है।
स्पष्टीकरण -
क्योंकि यूक्लिडियन ज्यामिति केवल समतल में मौजूद आकृतियों के लिए मान्य है लेकिन घुमावदार सतहों पर यह विफल हो जाती है।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित पद की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
रेखाखंड
निम्नलिखित पद की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
वर्ग
आकृति में, यदि AC = BD है, तो सिद्ध कीजिए कि AB = CD है।

यूक्लिड के कथन, सभी समकोण एक दूसरे के बराबर होते हैं, निम्नलिखित के रूप में दिया गया है :
‘रेखाएँ समांतर होती हैं, यदि वे प्रतिच्छेद नहीं करती’ का कथन, निम्नलिखित के रूप में दिया गया है :
यूक्लिड की पाँचवीं अभिधारणा को अन्य अभिधारणाओं और अभिगृहीतों का प्रयोग करते हुए, सिद्ध करने के प्रयासों के फलस्वरूप अन्य अनेक ज्यामितियों की खोज हुई।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
निम्नलिखित आकृति में, हमें प्राप्त है :
BX = `1/2` AB, BY = `1/2` BC तथा AB = BC है। दर्शाइए कि BX = BY है।
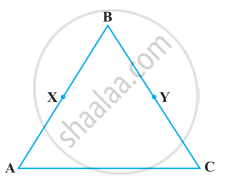
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
निम्नलिखित आकृति में, ∠1 = ∠2 और ∠2 = ∠3 है। दर्शाइए कि ∠1 = ∠3 है।
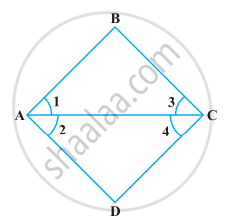
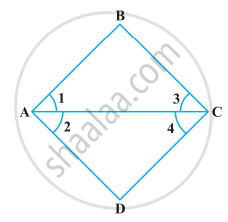
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
निम्नलिखित आकृति में, ∠1 = ∠3 और ∠2 = ∠4 है। दर्शाइए कि ∠A = ∠C है।
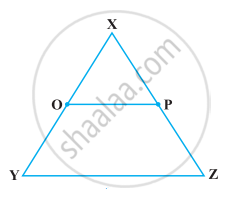
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
निम्नलिखित आकृति में, यदि OX = `1/2` XY, PX = `1/2` XZ और OX = PX हो, तो दर्शाइए कि XY = XZ है।