Advertisements
Advertisements
नीचे दिए गए बिंदु एकरेखीय हैं या नहीं? इसकी जाँच कीजिए।
A(1, −3), B(2, −5), C(−4, 7)
Concept: दूरी सूत्र
समलंब चतुर्भुज ABCD में, भुजा AB || भुजा PQ || भुजा DC, यदि AP = 15, PD = 12, QC = 14 तो BQ का मान ज्ञात कीजिए।

Concept: तीन समांतर रेखाएँ तथा उनकी तिर्यक रेखा का गुणधर्म (Property of Three Parallel Lines and Their Transversal)
ΔABC में B – D – C और BD = 7, BC = 20, तो निम्नलिखित अनुपात ज्ञात कीजिए।
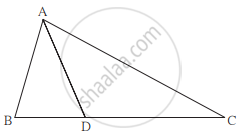
`(A(∆ABD))/(A(∆ABC))`
Concept: समरूप त्रिभुजों के क्षेत्रफलों का प्रमेय (Theorem of Areas of Similar Triangles)
दी गई आकृति में, रेख AC तथा रेख BD एक-दूसरे को बिंदु P पर प्रतिच्छेदित करते हैं।
यदि `(AP)/(CP) = (BP)/(DP)` हो, तो ΔABP ∼ ΔCDP सिद्ध करने के लिए निम्न कृति पूर्ण करो:
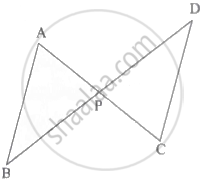
कृति: ΔABP तथा ΔCDP में,
`(AP)/(CP) = (BP)/(DP)` ..........`square`
∠APB ≅ `square` ...(शीर्षाभिमुख कोण)
∴ `square` ∼ ΔCDP ... (समरूपता की `square` कसोटी)
Concept: त्रिभुजों की समरूपता की कसौटियाँ
यदि ΔABC ∼ΔPQR, AB : PQ = 4 : 5 तथा A(ΔPQR) = 125 सेमी2 हो, तो A(ΔABC) का मान ज्ञात करो.
Concept: समरूप त्रिभुजों के क्षेत्रफलों का प्रमेय (Theorem of Areas of Similar Triangles)
ΔABC में, रेख XY || रेख AC. यदि 2AX = 3BX तथा XY = 9 हो, तो AC का मान ज्ञात करो।
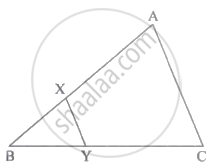
Concept: त्रिभुजों की समरूपता की कसौटियाँ
□ABCD समांतर चतुर्भुज है। बिंदु P, भुजा CD का मध्यबिंदु है। रेख BP यह विकर्ण AC को बिंदु X पर प्रतिच्छेदित करती है, तो सिद्ध करो कि 3AX = 2AC.
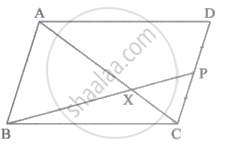
Concept: त्रिभुजों की समरूपता की कसौटियाँ
यदि ΔABC ∼ ΔPQR तथा `("A"(Delta"ABC"))/("A"(Delta"PQR")) = 16/25`, हो, तो AB : PQ का मान ज्ञात कीजिए।
Concept: समरूप त्रिभुजों के क्षेत्रफलों का प्रमेय (Theorem of Areas of Similar Triangles)
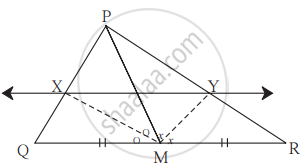
ΔPQR में, रेख PM माध्यिका है। ∠PMQ तथा ∠PMR के कोण समद्विभाजक भुजा PQ तथा भुजा PR को क्रमश: बिन्दु X तथा बिन्दु Y पर प्रतिच्छेदित करते हैं, तो सिद्ध कीजिए कि, XY || QR।
दिए गए रिक्त स्थानों की पूर्ति कर उपपत्ति पूर्ण कीजिए।
हल:
ΔPMQ में,
किरण MX यह ∠PMQ की समद्विभाजक है।
∴ `"MP"/"MQ" = square/square` .............(I) (कोण समद्विभाजक प्रमेय से)
उसी प्रकार, ΔPMR में,
किरण MY यह ∠PMR की समद्विभाजक है।
∴ `"MP"/"MR" = square/square` .............(II) (कोण समद्विभाजक प्रमेय से)
परंतु `"MP"/"MQ" = "MP"/"MR"` ................(III) (बिन्दु M यह QR का मध्यबिन्दु है अर्थात MQ = MR)
∴ `"PX"/square = square/"YR"` ............[(I), (II) व (III) से]
∴ XY || QR ...........(समानुपात के मूलभूत प्रमेय का विलोम)
Concept: त्रिभुज के कोण समद्विभाजक का प्रमेय
ΔABC में रेख DE || भुजा BC | यदि 2A(ΔADE) = A(⬜ DBCE), तो AB : AD का मान ज्ञात कीजिए तथा सिद्ध कीजिए BC = `sqrt3` DE |
Concept: समरूप त्रिभुजों के क्षेत्रफलों का प्रमेय (Theorem of Areas of Similar Triangles)
सिद्ध कीजिए “यदि किसी त्रिभुज की किसी एक भुजा के समांतर खींची गईं रेखा उसकी अन्य दो भुजाओं को दो भिन्न बिन्दुओं पर प्रतिच्छेदित करे तो वह रेखा अन्य दो भुजाओं को समान अनुपात में विभाजित करती है।
Concept: समानुपात का मूलभूत प्रमेय (Basic Proportionality Theorem)
यदि Δ ABC और ~ Δ PQR और AB : PQ = 2 : 3 तो `(A(Δ "ABC"))/(A(Δ "PQR")` का मान ज्ञात कीजिए।
Concept: समरूप त्रिभुजों के क्षेत्रफलों का प्रमेय (Theorem of Areas of Similar Triangles)
`square`ABCD एक समलंब चतुर्भुज है। AB || CD समलंब `square`ABCD के विकर्ण परस्पर बिंदु P में प्रतिच्छेदित करते हैं।
इस आधार पर नीचे दिए प्रश्नों के उत्तर लिखिए:
- दी गई जानकारी के आधार पर आकृति बनाइये।
- उस आधार पर एकांतर कोणों की तथा शीर्षाभिमुख कोणों की जोड़ियाँ लिखिए।
- समरूपता की कसौटीसह समरूप त्रिभुओं के नाम लिखिए।
Concept: त्रिभुजों की समरूपता की कसौटियाँ

ΔABC में, किरण BD यह ∠ABC का कोण समद्विभाजक है। A - D - C, रेख DE || भुजा BC, A - E - B हो, तो सिद्ध कीजिए `("AB")/("BC") = ("AE")/("EB")`
उपपत्ति:
ΔABC में, किरण BD यह ∠B को समद्विभाजित करता है।
∴ `square/("BC") = ("AD")/("DC")` ......(I) (`square`)
ΔABC में, DE || BC
∴ `(square)/("EB") = ("AD")/("DC")` ....(II) (`square`)
∴ `("AB")/square = square/("EB")` [(I) व (II) से]
Concept: त्रिभुज के कोण समद्विभाजक का प्रमेय
आकृति में ∠MNP = 90°, रेख NQ ⊥ रेख MP, MQ = 9, QP = 4, तो NQ का मान ज्ञात कीजिए।
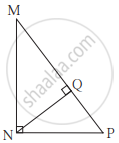
Concept: 30°-60°-90° माप वाले त्रिभुज का गुणधर्म
किसी आयत की लंबाई 35 सेमी तथा चौड़ाई 12 सेमी हो तो उस आयत के विकर्ण की लंबाई ज्ञात कीजिए।
Concept: पायथागोरस का प्रमेय (Theorem of Pythagoras)
निम्नलिखित में से कौन-सा पायथागोरस का त्रिक् है?
Concept: पायथागोरस के त्रिक्
निम्नलिखित बहुवैकल्पिक प्रश्न के दिए गए उत्तरों में से उचित विकल्प चुनकर लिखिए।
निम्नलिखित में से कौन-से दिनांक की संख्या पायथागोरस का त्रिक् हैं?
Concept: पायथागोरस के त्रिक्
किसी समकोण त्रिभुज में समकोण बनाने वाली भुजाएँ क्रमश: 9 सेमी तथा 12 सेमी हों तो उस त्रिभुज के कर्ण की लंबाई ज्ञात कीजिए।
Concept: पायथागोरस का प्रमेय (Theorem of Pythagoras)
ΔABC में रेख AP माध्यिका है। यदि BC = 18, AB2 + AC2 = 260 तो AP ज्ञात कीजिए।
Concept: अपोलोनियस का प्रमेय (Appollonius’ Theorem)
