Shortest Distance Between Two Lines

Vector Form:

\[\mathbf{d}=\left|\frac{(\overline{\mathbf{b}}_{1}\times\overline{\mathbf{b}}_{2}).(\overline{\mathbf{a}}_{2}-\overline{\mathbf{a}}_{1})}{\left|\overline{\mathbf{b}}_{1}\times\overline{\mathbf{b}}_{2}\right|}\right|\]

Cartesian Form:

\[\mathbf{d}=\left|\frac{ \begin{vmatrix} x_2-x_1 & y_2-y_1 & z_2-z_1 \\ \mathbf{a}_1 & \mathbf{b}_1 & \mathbf{c}_1 \\ \mathbf{a}_2 & \mathbf{b}_2 & \mathbf{c}_2 \end{vmatrix}}{\sqrt{\left(\mathbf{a}_1\mathbf{b}_2-\mathbf{a}_2\mathbf{b}_1\right)^2+\left(\mathbf{a}_1\mathbf{c}_2-\mathbf{a}_2\mathbf{c}_1\right)^2+\left(\mathbf{b}_1\mathbf{c}_2-\mathbf{b}_2\mathbf{c}_1\right)^2}}\right|\]

If two lines in space intersect at a point, then the shortest distance between them is zero. Also, if two lines in space are parallel, then the shortest distance between them will be the perpendicular distance, i.e. the length of the perpendicular drawn from a point on one line onto the other line. Further, in a space, there are lines which are neither intersecting nor parallel. In fact, such pair of lines are non coplanar and are called skew lines.Fig.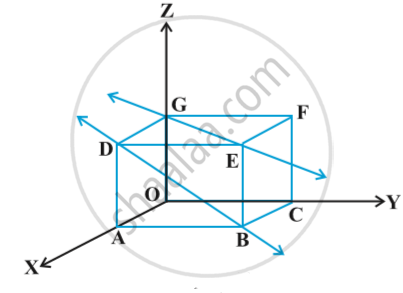

The line GE that goes diagonally across the ceiling and the line DB passes through one corner of the ceiling directly above A and goes diagonally down the wall. These lines are skew because they are not parallel and also never meet. 
By the shortest distance between two lines we mean the join of a point in one line with one point on the other line so that the length of the segment so obtained is the smallest. 
For skew lines, the line of the shortest distance will be perpendicular to both the lines.

Distance between two skew lines:
We now determine the shortest distance between two skew lines in the following way: Let `l_1` and `l_2`  be two skew lines with equations in fig.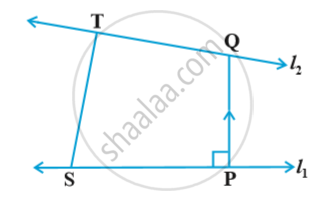

`vec r = vec a _1 + lambda vec b_1`     ...(1)
and `vec r = vec a _2 + mu vec b _2`    ...(2)
Take any point S on `l_1`with position vector `vec a_1`  and T on `l_2`, with position vector `vec a_2`.  Then the magnitude of the shortest distance vector will be equal to that of the projection of ST along the direction of the line of shortest distance. 
If `vec (PQ)` is the shortest distance vector between `l_1` and `l_2` , then it being perpendicular to both `vec b_1` and `vec b_2` , the unit vector `hat n` along `vec (PQ)` would  therefore be 
`hat n = (vec b_1 xx vec b_2)/ |vec b_1 xx vec b_2|`   ...(3)
Then `vec (PQ) = d . hat n `
where, d is the magnitude of the shortest distance vector. Let θ be the angle between `vec (ST)`  and `vec (PQ).` Then 
`PQ = ST  |cos θ| `
But cos θ `= |(vec (PQ) . vec (ST))/(|vec (PQ)| |vec (ST)|)| `

`= |(d . hat n (vec a_2 - vec a_1)) / (d  ST)|`    (since `vec (ST) = vec a_2 - vec a_1`)

`= |((vec b _1 xx vec b_2) . (vec a_2 - vec a_1)) /( ST    |vec b_1 xx vec b_2|)|` [From (3)]
Hence, the required shortest distance is 
d = PQ =ST |cos θ| 
or d=` |((vec b_1 xx vec b_2) . (vec a_2 xx vec a_1))/(|vec b_1 xx vec b_2|)|`

The shortest distance between the lines
`l_1 : (x - x_1)/a_1 = (y - y_1)/b_1 = (z - z_1)/c_1`

and `l_2 : (x - x_2)/a_2 = (y - y_2)/b_2 = (z - z_2)/c_2`

is `||(x_2-x_1 , y_2 - y_1 , z_2 - z_1),(a_1 , b_1 , c_1), (a_2 , b_2 , c_2)|/ sqrt ((b_1c_2 - b_2c_1)^2 + (c_1a_2 - c_2a_1)^2 + (a_1b_2 - a_2b_1)^2) |`

Video link : https://youtu.be/BXzj9mJvTKQ

Distance between parallel lines: 
If two lines `l_1` and  `l_2` are parallel, then they are coplanar.  Let the lines be given by 
`vec r = vec a_1 + lambda vec b`   ...(1)
and `vec r = vec a_2 + mu vec b`  ...(2)
where , `vec a_1` is the position vector of a point S on `l_1` and `vec a_2` is the position vector of a point T on `l_2` in following fig. 

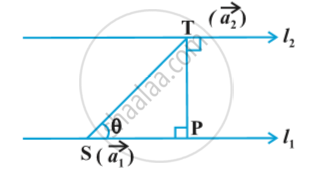
As `l_1, l_2` are coplanar, if the foot of the perpendicular from T on the line `l_1` is P, then the distance between the lines `l_1` and `l_2` =  |TP|.
Let θ be the angle between the vectors `vec (ST)` and `vec b`. Then 

`vec b xx vec (ST) = ( |vec b|  |vec (ST)|  sin θ)  hat n `    ...(3)

where `hat n` is the unit vector perpendicular to the plane of the lines `l_1` and `l_2` But `vec (ST) = vec a_2 -vec a_1`

Therefore, from (3), we get 
`vec b xx (vec a_2 - vec a_1) = |vec b|  PT  hat n`  (since PT =ST sin θ )
i.e. `|vec b xx (vec a_2 - vec a_1)| = |vec b| PT . 1`  (as `|hat n|` = 1)
Hence, the distance between the given parallel lines is
`d = |vec (PT)| = |(vec b xx (vec a_2 - vec a _1))/|vec b||`

\[SD=\left|\frac{\left(a_{2}-a_{1}\right)\times b}{\left|b\right|}\right|\]