Advertisements
Advertisements
प्रश्न
A(-1, 1), B(5, -3) आणि C(3, 5) हे शिरोबिंदू असलेल्या त्रिकोणाच्या मध्यगांच्या लांबी काढा.
उत्तर
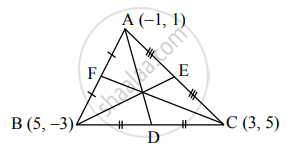
समजा, AD, BE व CF ह्या त्रिकोणाच्या मध्यगा आहेत.
∴ बिंदू D, E व F अनुक्रमे बाजू BC, AC व AB चे मध्यबिंदू आहेत.
∴ मध्यबिंदूच्या सूत्रानुसार,
D चे निर्देशक = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
= `((5 + 3)/2, (-3 + 5)/2) = (8/2, 2/2)`
D चे निर्देशक = (4, 1)
E चे निर्देशक = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
= `((-1 + 3)/2, (1 + 5)/2) = (2/2, 6/2)`
E चे निर्देशक = (1, 3)
F चे निर्देशक = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
= `((-1 + 5)/2, (1 - 3)/2) = (4/2, (-2)/2)`
F चे निर्देशक = (2, -1)
अंतराच्या सूत्रानुसार,
d(A, D) = `sqrt((-1 - 4)^2 + (1 - 1)^2)`
= `sqrt((-5)^2 + 0^2) = sqrt25 = 5`
d(B, E) = `sqrt((5 - 1)^2 + (-3 - 3)^2)`
= `sqrt(4^2 + (-6)^2) = sqrt(16 + 36) = sqrt52 = 2sqrt13`
d(C, F) = `sqrt((3 - 2)^2 + [5 - (-1)]^2)`
= `sqrt(1^2 + (5 + 1)^2)`
= `sqrt(1 + 36) = sqrt37`
∴ दिलेल्या त्रिकोणाच्या मध्यगांची लांबी 5 एकक, `2sqrt13` एकक व `sqrt37` एकक आहे.
APPEARS IN
संबंधित प्रश्न
रेख AB हा वर्तुळाचा व्यास असून बिंदू P हे केंद्र आहे. A(2, -3)आणि P (-2, 0) असल्यास B बिंदूचे निर्देशक काढा.
(22, 20) आणि (0, 16) यांना जोडणाऱ्या रेषाखंडाच्या मध्यबिंदूचे निर्देशक काढा.
P(0,6) आणि Q(12,20) यांना जोडणाऱ्या रेषाखंडाच्या मध्यबिंदूचे निर्देशक काढा.
समांतरभुज चौकोनाच्या तीन शिरोबिंदूंचे निर्देशक A(5,6), B(1,-2) आणि C(3,-2) असतील तर चौथ्या बिंदूच्या निर्देशकांच्या शक्य त्या सर्व जोड्या काढा.
रेख AB वरील बिंदू P, Q, R व S यांच्यामुळे त्या रेषाखंडाचे पाच एकरूप भाग होतात. जर A-P-Q – R-S-B आणि Q(12, 14), S(4, 18); तर A, P, R आणि B चे निर्देशक काढा.
जर D(-7, 6), E(8, 5) आणि F(2, -2) हे त्रिकोणाच्या बाजूंचे मध्यबिंदू असतील, तर त्या त्रिकोणाच्या मध्यगा संपातबिंदूचे निर्देशक काढा.
P(1, –2), Q(5, 2), R(3, –1), S(–1, –5) हे समांतरभुज चौकोनाचे शिरोबिंदू आहेत, हे दाखवा.
जर A(–4, 2) आणि B(6, 2) यांना जोडणाऱ्या रेषाखंडाचा मध्यबिंदू P असेल, तर P चे निर्देशक ______
A(-4, 2) व B(6, 2) या बिंदूंना जोडणाऱ्या रेषाखंडाच्या बिंदू P हा मध्यबिंदू आहे. तर P बिंदूचे निर्देशक काढण्यासाठी कृती पूर्ण करा.
उकल:

(-4, 2) = (x1, y1), (6, 2) = (x2, y2) आणि बिंदू P चे निर्देशक (x, y) मानू
मध्यबिंदूच्या सूत्रानुसार,
`x = (x_1 + x_2)/2`
∴ `x = (square + 6)/2`
∴ `x = square/2`
∴ x = `square`
`y = (y_1 + y_2)/2`
∴ `y = (2 + square)/2`
∴ y = `4/2`
∴ y = `square`
∴ मध्यबिंदू P चे निर्देशक `square` आहेत.
