Advertisements
Advertisements
प्रश्न
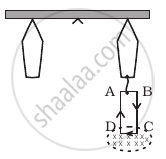
A 100 turn rectangular coil ABCD (in XY plane) is hung from one arm of a balance (Figure). A mass 500 g is added to the other arm to balance the weight of the coil. A current 4.9 A passes through the coil and a constant magnetic field of 0.2 T acting inward (in xz plane) is switched on such that only arm CD of length 1 cm lies in the field. How much additional mass ‘m’ must be added to regain the balance?
उत्तर
Here we use the concept of magnetic force on straight current-carrying conductor placed in the region of external uniform magnetic field. The magnetic force exerted on CD due to external magnetic field must balance its weight.
And spring balance to be in equilibrium net torque should also be equal to zero.
At t = 0, the external magnetic field is off. Let us consider the separation of each hung from mid-point be `l`.
`Mgl = W_("coil")l`
`0.5 gl = W_("coil") l`
`W_("coil") = 0.5 xx 9.8 N`
By taking moment of force about mid-point, we get the weight of coil.
And Let `'m` be the mass which is added to regain the balance.
When the magnetic field is switched on.
`Mgl + mgl = W_("coil") l + (ILB sin 90^circ)l`
`Mgl = (ILB)l`
`m = (BIL)/g = (0.2 xx 4.9 xx 1 xx 10^-2)/9.8 = 10^-3 kg = 1g`
Therefore, 1 g of additional mass must be added to regain the balance.
APPEARS IN
संबंधित प्रश्न
A rod of length l is moved horizontally with a uniform velocity 'v' in a direction perpendicular to its length through a region in which a uniform magnetic field is acting vertically downward. Derive the expression for the emf induced across the ends of the rod.
Choose the correct alternative and rewrite the following:
What will happen to the current passing through a resistance, if the potential difference across it is doubled and the resistance is halved?
A proton enters into a magnetic field of induction 1.732 T, with a velocity of 107 m/s at an angle 60° to the field. The force acting on the proton is e = 1.6 × 10-19 C, sin 60° = cos 30° = `sqrt3/2`
A magnetic field set up using Helmholtz coils is uniform in a small region and has a magnitude of 0.75 T. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through 15 kV enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is 9.0 × 10–5 V m–1, make a simple guess as to what the beam contains. Why is the answer not unique?
A cubical region of space is filled with some uniform electric and magnetic fields. An electron enters the cube across one of its faces with velocity v and a positron enters via opposite face with velocity – v. At this instant ______.
- the electric forces on both the particles cause identical accelerations.
- the magnetic forces on both the particles cause equal accelerations.
- both particles gain or loose energy at the same rate.
- the motion of the centre of mass (CM) is determined by B alone.
A charge particle moves along circular path in a uniform magnetic field in a cyclotron. The kinetic energy of the charge particle increases to 4 times its initial value. What will be the ratio of new radius to the original radius of circular path of the charge particle:
Two long current-carrying conductors are placed parallel to each other at a distance of 8 cm between them. The magnitude of the magnetic field produced at the mid-point between the two conductors due to the current flowing in them is 300µT. The equal current flowing in the two conductors is ______.
With a neat labelled diagram, explain cyclotron motion and cyclotron formula.
Distinguish between the forces experienced by a moving charge in a uniform electric field and in a uniform magnetic field. (Any two points)
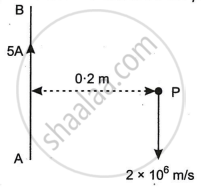
A long straight wire AB carries a current of 5A. P is a proton travelling with a velocity of 2 × 106 m/s, parallel to the wire, 0.2 m from it and in a direction opposite to the current, as shown in Figure below. Calculate the force which magnetic field of the current carrying conductor AB exerts on the proton.