Advertisements
Advertisements
प्रश्न
A 13 m long ladder is leaning against a wall, touching the wall at a certain height from the ground level. The bottom of the ladder is pulled away from the wall, along the ground, at the rate of 2 m/s. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall?
उत्तर
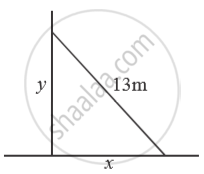
`x^2 + y^2 = 169` ...(i)
The bottom of the ladder is beign pulled, so these distances are changing with time,
`2x dx/dt + 2y dy/dt =0` ...(ii)
`dy/dt = - x/y dx/dt` .....(iii)
at x=5m then from (i) y=12m
From equation(iii)
`dy/dt = -5/12xx2`
`dy/dt = - 5/6 m//s`
– sign indicates the height is decreasing.
APPEARS IN
संबंधित प्रश्न
Find the rate of change of the area of a circle with respect to its radius r when r = 3 cm.
Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7.
The volume of a sphere is increasing at the rate of 3 cubic centimeter per second. Find the rate of increase of its surface area, when the radius is 2 cm
The total cost C(x) associated with the production of x units of an item is given by C(x) = 0.005x3 – 0.02x2 + 30x + 5000. Find the marginal cost when 3 units are produced, whereby marginal cost we mean the instantaneous rate of change of total cost at any level of output.
Find the rate of change of the total surface area of a cylinder of radius r and height h, when the radius varies?
Find the rate of change of the volume of a ball with respect to its radius r. How fast is the volume changing with respect to the radius when the radius is 2 cm?
The total revenue received from the sale of x units of a product is given by R (x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7 ?
The money to be spent for the welfare of the employees of a firm is proportional to the rate of change of its total revenue (Marginal revenue). If the total revenue (in rupees) recieved from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5, find the marginal revenue, when x = 5, and write which value does the question indicate ?
A ladder 13 m long leans against a wall. The foot of the ladder is pulled along the ground away from the wall, at the rate of 1.5 m/sec. How fast is the angle θ between the ladder and the ground is changing when the foot of the ladder is 12 m away from the wall.
Find an angle θ which increases twice as fast as its cosine ?
The radius of a cylinder is increasing at the rate 2 cm/sec. and its altitude is decreasing at the rate of 3 cm/sec. Find the rate of change of volume when radius is 3 cm and altitude 5 cm.
A kite is 120 m high and 130 m of string is out. If the kite is moving away horizontally at the rate of 52 m/sec, find the rate at which the string is being paid out.
The volume of a spherical balloon is increasing at the rate of 25 cm3/sec. Find the rate of change of its surface area at the instant when radius is 5 cm ?
If a particle moves in a straight line such that the distance travelled in time t is given by s = t3 − 6t2+ 9t + 8. Find the initial velocity of the particle ?
The side of a square is increasing at the rate of 0.1 cm/sec. Find the rate of increase of its perimeter ?
If the rate of change of volume of a sphere is equal to the rate of change of its radius, find the radius of the sphere ?
The distance moved by a particle travelling in straight line in t seconds is given by s = 45t + 11t2 − t3. The time taken by the particle to come to rest is
If the rate of change of volume of a sphere is equal to the rate of change of its radius, then its radius is equal to
If the rate of change of area of a circle is equal to the rate of change of its diameter, then its radius is equal to
A ladder 13 m long is leaning against a vertical wall. The bottom of the ladder is dragged away from the wall along the ground at the rate of 2 cm/sec. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall.
Two men A and B start with velocities v at the same time from the junction of two roads inclined at 45° to each other. If they travel by different roads, find the rate at which they are being seperated.
A man, 2m tall, walks at the rate of `1 2/3` m/s towards a street light which is `5 1/3`m above the ground. At what rate is the tip of his shadow moving? At what rate is the length of the shadow changing when he is `3 1/3`m from the base of the light?
A swimming pool is to be drained for cleaning. If L represents the number of litres of water in the pool t seconds after the pool has been plugged off to drain and L = 200 (10 – t)2. How fast is the water running out at the end of 5 seconds? What is the average rate at which the water flows out during the first 5 seconds?
Total revenue in rupees received from the sale of x units of a product is given by R(x)= 3x2+ 36x + 5. The marginal revenue, when x = 15 is ____________.
Let y = f(x) be a function. If the change in one quantity 'y’ varies with another quantity x, then which of the following denote the rate of change of y with respect to x.
If equal sides of an isosceles triangle with fixed base 10 cm are increasing at the rate of 4 cm/sec, how fast is the area of triangle increasing at an instant when all sides become equal?
