Advertisements
Advertisements
प्रश्न
If equal sides of an isosceles triangle with fixed base 10 cm are increasing at the rate of 4 cm/sec, how fast is the area of triangle increasing at an instant when all sides become equal?
उत्तर
Given, side is increasing at the rate of 4 cm/sec.
Let equal sides are of length x cm.
∴ `dx/dt` = 4 cm/sec
∵ Area of isosceles triangle is `b/2 sqrt(a^2 - b^2/4)`
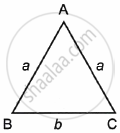
∵ b = 10 cm and a = x
`\implies` A = `10/2 sqrt(x^2 - (10)^2/4`
`\implies` A = `5sqrt(x^2 - 25)`
`\implies (dA)/dt = 5/2 (2x)/sqrt(x^2 - 25) dx/dt`
`(dA)/dt = (5x)/sqrt(x^2 - 25) dx/dt`
∵ x = 10 ...(when all sides become equal)
`\implies (dA)/dt = (5 xx 10)/sqrt(100 - 25) xx 4`
= `(50 xx 4)/sqrt(75) = (50 xx 4)/(5sqrt(3))`
`(dA)/dt = 40/sqrt(3)`
APPEARS IN
संबंधित प्रश्न
The Volume of cube is increasing at the rate of 9 cm 3/s. How fast is its surfacee area increasing when the length of an edge is 10 cm?
The rate of growth of bacteria is proportional to the number present. If, initially, there were
1000 bacteria and the number doubles in one hour, find the number of bacteria after 2½
hours.
[Take `sqrt2` = 1.414]
The radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
The radius of an air bubble is increasing at the rate `1/2` cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
The total cost C(x) in rupees associated with the production of x units of an item is given by C(x) = 0.007x3 – 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced
Find the rate of change of the volume of a sphere with respect to its diameter ?
Find the rate of change of the area of a circle with respect to its radius r when r = 5 cm
The total cost C (x) associated with the production of x units of an item is given by C (x) = 0.007x3 − 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced ?
The radius of a spherical soap bubble is increasing at the rate of 0.2 cm/sec. Find the rate of increase of its surface area, when the radius is 7 cm.
A balloon which always remains spherical, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon is increasing when the radius is 15 cm.
A stone is dropped into a quiet lake and waves move in circles at a speed of 4 cm/sec. At the instant when the radius of the circular wave is 10 cm, how fast is the enclosed area increasing?
A man 160 cm tall, walks away from a source of light situated at the top of a pole 6 m high, at the rate of 1.1 m/sec. How fast is the length of his shadow increasing when he is 1 m away from the pole?
A ladder 13 m long leans against a wall. The foot of the ladder is pulled along the ground away from the wall, at the rate of 1.5 m/sec. How fast is the angle θ between the ladder and the ground is changing when the foot of the ladder is 12 m away from the wall.
A particle moves along the curve y = x3. Find the points on the curve at which the y-coordinate changes three times more rapidly than the x-coordinate.
Find an angle θ whose rate of increase twice is twice the rate of decrease of its cosine ?
The top of a ladder 6 metres long is resting against a vertical wall on a level pavement, when the ladder begins to slide outwards. At the moment when the foot of the ladder is 4 metres from the wall, it is sliding away from the wall at the rate of 0.5 m/sec. How fast is the top-sliding downwards at this instance?
How far is the foot from the wall when it and the top are moving at the same rate?
The radius of a cylinder is increasing at the rate 2 cm/sec. and its altitude is decreasing at the rate of 3 cm/sec. Find the rate of change of volume when radius is 3 cm and altitude 5 cm.
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of the perimeter.
If a particle moves in a straight line such that the distance travelled in time t is given by s = t3 − 6t2+ 9t + 8. Find the initial velocity of the particle ?
Find the surface area of a sphere when its volume is changing at the same rate as its radius ?
The amount of pollution content added in air in a city due to x diesel vehicles is given by P(x) = 0.005x3 + 0.02x2 + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added and write which value is indicated in the above questions ?
The radius of a sphere is changing at the rate of 0.1 cm/sec. The rate of change of its surface area when the radius is 200 cm is
The radius of the base of a cone is increasing at the rate of 3 cm/minute and the altitude is decreasing at the rate of 4 cm/minute. The rate of change of lateral surface when the radius = 7 cm and altitude 24 cm is
Two men A and B start with velocities v at the same time from the junction of two roads inclined at 45° to each other. If they travel by different roads, find the rate at which they are being seperated.
A ladder, 5 meter long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then the rate at which the angle between the floor and the ladder is decreasing when lower end of ladder is 2 metres from the wall is ______.
A spherical balloon is being inflated at the rate of 35 cc/min. The rate of increase in the surface area (in cm2/min.) of the balloon when its diameter is 14 cm, is ______.
The median of an equilateral triangle is increasing at the ratio of `2sqrt(3)` cm/s. Find the rate at which its side is increasing.
A kite is being pulled down by a string that goes through a ring on the ground 8 meters away from the person pulling it. If the string is pulled in at 1 meter per second, how fast is the kite coming down when it is 15 meters high?
