Advertisements
Advertisements
प्रश्न
If equal sides of an isosceles triangle with fixed base 10 cm are increasing at the rate of 4 cm/sec, how fast is the area of triangle increasing at an instant when all sides become equal?
उत्तर
Given, side is increasing at the rate of 4 cm/sec.
Let equal sides are of length x cm.
∴ `dx/dt` = 4 cm/sec
∵ Area of isosceles triangle is `b/2 sqrt(a^2 - b^2/4)`
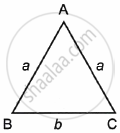
∵ b = 10 cm and a = x
`\implies` A = `10/2 sqrt(x^2 - (10)^2/4`
`\implies` A = `5sqrt(x^2 - 25)`
`\implies (dA)/dt = 5/2 (2x)/sqrt(x^2 - 25) dx/dt`
`(dA)/dt = (5x)/sqrt(x^2 - 25) dx/dt`
∵ x = 10 ...(when all sides become equal)
`\implies (dA)/dt = (5 xx 10)/sqrt(100 - 25) xx 4`
= `(50 xx 4)/sqrt(75) = (50 xx 4)/(5sqrt(3))`
`(dA)/dt = 40/sqrt(3)`
APPEARS IN
संबंधित प्रश्न
If y = f (u) is a differential function of u and u = g(x) is a differential function of x, then prove that y = f [g(x)] is a differential function of x and `dy/dx=dy/(du) xx (du)/dx`
A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm/s. At the instant when the radius of the circular wave is 8 cm, how fast is the enclosed area increasing?
A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15 cm.
The radius of an air bubble is increasing at the rate `1/2` cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
The rate of change of the area of a circle with respect to its radius r at r = 6 cm is ______.
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5. The marginal revenue, when x = 15 is ______.
The total cost C(x) associated with the production of x units of an item is given by C(x) = 0.005x3 – 0.02x2 + 30x + 5000. Find the marginal cost when 3 units are produced, whereby marginal cost we mean the instantaneous rate of change of total cost at any level of output.
Find the rate of change of the volume of a sphere with respect to its surface area when the radius is 2 cm ?
Find the rate of change of the area of a circular disc with respect to its circumference when the radius is 3 cm ?
The money to be spent for the welfare of the employees of a firm is proportional to the rate of change of its total revenue (Marginal revenue). If the total revenue (in rupees) recieved from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5, find the marginal revenue, when x = 5, and write which value does the question indicate ?
A man 180 cm tall walks at a rate of 2 m/sec. away, from a source of light that is 9 m above the ground. How fast is the length of his shadow increasing when he is 3 m away from the base of light?
Find an angle θ which increases twice as fast as its cosine ?
The top of a ladder 6 metres long is resting against a vertical wall on a level pavement, when the ladder begins to slide outwards. At the moment when the foot of the ladder is 4 metres from the wall, it is sliding away from the wall at the rate of 0.5 m/sec. How fast is the top-sliding downwards at this instance?
How far is the foot from the wall when it and the top are moving at the same rate?
Sand is being poured onto a conical pile at the constant rate of 50 cm3/ minute such that the height of the cone is always one half of the radius of its base. How fast is the height of the pile increasing when the sand is 5 cm deep ?
A circular disc of radius 3 cm is being heated. Due to expansion, its radius increases at the rate of 0.05 cm/sec. Find the rate at which its area is increasing when radius is 3.2 cm.
The radius of a circle is increasing at the rate of 0.5 cm/sec. Find the rate of increase of its circumference ?
A ladder, 5 metre long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides down wards at the rate of 10 cm/sec, then find the rate at which the angle between the floor and ladder is decreasing when lower end of ladder is 2 metres from the wall ?
The radius of a sphere is changing at the rate of 0.1 cm/sec. The rate of change of its surface area when the radius is 200 cm is
A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of
Water is dripping out from a conical funnel of semi-vertical angle `pi/4` at the uniform rate of 2cm2/sec in the surface area, through a tiny hole at the vertex of the bottom. When the slant height of cone is 4 cm, find the rate of decrease of the slant height of water.
The rate of change of volume of a sphere with respect to its surface area, when the radius is 2 cm, is ______.
A kite is moving horizontally at a height of 151.5 meters. If the speed of kite is 10 m/s, how fast is the string being let out; when the kite is 250 m away from the boy who is flying the kite? The height of boy is 1.5 m.
The sides of an equilateral triangle are increasing at the rate of 2 cm/sec. The rate at which the area increases, when side is 10 cm is ______.
The instantaneous rate of change at t = 1 for the function f (t) = te-t + 9 is ____________.
Let y = f(x) be a function. If the change in one quantity 'y’ varies with another quantity x, then which of the following denote the rate of change of y with respect to x.
The radius of a circle is increasing uniformly at the rate of 3 cm per second. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
A spherical balloon is filled with 4500π cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of 72π cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases 49 minutes after the leakage began is ______.
A particle moves along the curve 3y = ax3 + 1 such that at a point with x-coordinate 1, y-coordinate is changing twice as fast at x-coordinate. Find the value of a.
