Advertisements
Advertisements
प्रश्न
A kite is moving horizontally at a height of 151.5 meters. If the speed of kite is 10 m/s, how fast is the string being let out; when the kite is 250 m away from the boy who is flying the kite? The height of boy is 1.5 m.
Advertisements
उत्तर
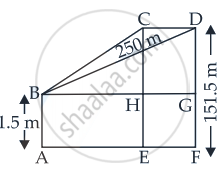
Given that height of the kite (h) = 151.5 m
Speed of the kite(V) = 10 m/s
Let FD be the height of the kite and AB be the height of the boy.
Let AF = xm
∴ BG = AF = xm
And `"dx"/"dt"` = 10 m/s
From the figure, we get that
GD = DF – GF
⇒ DF – AB
= (151.5 – 1.5) m = 150 m ......[∵ AB = GF]
Now in ΔBGD,
BG2 + GD2 = BD2 ......(By Pythagoras Theorem)
⇒ x2 + (150)2 = (250)2
⇒ x2 + 22500 = 62500
⇒ x2 = 62500 – 22500
⇒ x2 = 40000
⇒ x2 = 40000
Let initially the length of the string be y m
∴ In ΔBGD
BG2 + GD2 = BD2
⇒ x2 + (150)2 = y2
Differentiating both sides w.r.t., t, we get
⇒ `2x * "dx"/"dt" + 0 = 2y * "dy"/"dt"` ......`[because "dx"/"dt" = 10 "m"/"s"]`
⇒ 2 × 200 × 10 = 2 × 250 × `"dy"/"dt"`
∴ `"dy"/"dt" = (2 xx 200 xx 10)/(2 xx 250)` = 8 m/s
Hence, the rate of change of the length of the string is 8 m/s.
APPEARS IN
संबंधित प्रश्न
If y = f (u) is a differential function of u and u = g(x) is a differential function of x, then prove that y = f [g(x)] is a differential function of x and `dy/dx=dy/(du) xx (du)/dx`
Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
The rate of change of the area of a circle with respect to its radius r at r = 6 cm is ______.
The volume of a sphere is increasing at the rate of 8 cm3/s. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
The volume of a sphere is increasing at the rate of 3 cubic centimeter per second. Find the rate of increase of its surface area, when the radius is 2 cm
An edge of a variable cube is increasing at the rate of 3 cm per second. How fast is the volume of the cube increasing when the edge is 10 cm long?
The radius of a spherical soap bubble is increasing at the rate of 0.2 cm/sec. Find the rate of increase of its surface area, when the radius is 7 cm.
A man 160 cm tall, walks away from a source of light situated at the top of a pole 6 m high, at the rate of 1.1 m/sec. How fast is the length of his shadow increasing when he is 1 m away from the pole?
If y = 7x − x3 and x increases at the rate of 4 units per second, how fast is the slope of the curve changing when x = 2?
A particle moves along the curve y = x3. Find the points on the curve at which the y-coordinate changes three times more rapidly than the x-coordinate.
Find an angle θ which increases twice as fast as its cosine ?
Water is running into an inverted cone at the rate of π cubic metres per minute. The height of the cone is 10 metres, and the radius of its base is 5 m. How fast the water level is rising when the water stands 7.5 m below the base.
A man 2 metres high walks at a uniform speed of 6 km/h away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases ?
The radius of a cylinder is increasing at the rate 2 cm/sec. and its altitude is decreasing at the rate of 3 cm/sec. Find the rate of change of volume when radius is 3 cm and altitude 5 cm.
A kite is 120 m high and 130 m of string is out. If the kite is moving away horizontally at the rate of 52 m/sec, find the rate at which the string is being paid out.
Find the point on the curve y2 = 8x for which the abscissa and ordinate change at the same rate ?
If a particle moves in a straight line such that the distance travelled in time t is given by s = t3 − 6t2+ 9t + 8. Find the initial velocity of the particle ?
The amount of pollution content added in air in a city due to x diesel vehicles is given by P(x) = 0.005x3 + 0.02x2 + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added and write which value is indicated in the above questions ?
The radius of a sphere is changing at the rate of 0.1 cm/sec. The rate of change of its surface area when the radius is 200 cm is
A cone whose height is always equal to its diameter is increasing in volume at the rate of 40 cm3/sec. At what rate is the radius increasing when its circular base area is 1 m2?
For what values of x is the rate of increase of x3 − 5x2 + 5x + 8 is twice the rate of increase of x ?
The radius of the base of a cone is increasing at the rate of 3 cm/minute and the altitude is decreasing at the rate of 4 cm/minute. The rate of change of lateral surface when the radius = 7 cm and altitude 24 cm is
If the rate of change of area of a circle is equal to the rate of change of its diameter, then its radius is equal to
In a sphere the rate of change of surface area is
A 13 m long ladder is leaning against a wall, touching the wall at a certain height from the ground level. The bottom of the ladder is pulled away from the wall, along the ground, at the rate of 2 m/s. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall?
If the area of a circle increases at a uniform rate, then prove that perimeter varies inversely as the radius
What is the rate of change of the area of a circle with respect to its radius when, r = 3 cm
A cylindrical tank of radius 10 feet is being filled with wheat at the rate of 3/4 cubic feet per minute. The then depth of the wheat is increasing at the rate of
A spherical balloon is being inflated at the rate of 35 cc/min. The rate of increase in the surface area (in cm2/min.) of the balloon when its diameter is 14 cm, is ______.
A spherical balloon is filled with 4500π cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of 72π cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases 49 minutes after the leakage began is ______.
If the circumference of circle is increasing at the constant rate, prove that rate of change of area of circle is directly proportional to its radius.
If equal sides of an isosceles triangle with fixed base 10 cm are increasing at the rate of 4 cm/sec, how fast is the area of triangle increasing at an instant when all sides become equal?
What does evaluating \[\left.\frac{dy}{dx}\right|_{x=x_0}\] give?
When \(x\) and \(y\) both vary with respect to \(t\), which formula gives the rate of change of \(y\) with respect to \(x\)?
For the Chain Rule for Rates \[\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}\], which condition is required?
For a circle with area \[A=\pi r^2\], what is \[\frac{dA}{dr}\]?
Which procedure is used in related rates?
