Advertisements
Advertisements
Question
A kite is moving horizontally at a height of 151.5 meters. If the speed of kite is 10 m/s, how fast is the string being let out; when the kite is 250 m away from the boy who is flying the kite? The height of boy is 1.5 m.
Solution
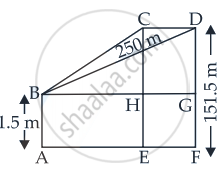
Given that height of the kite (h) = 151.5 m
Speed of the kite(V) = 10 m/s
Let FD be the height of the kite and AB be the height of the boy.
Let AF = xm
∴ BG = AF = xm
And `"dx"/"dt"` = 10 m/s
From the figure, we get that
GD = DF – GF
⇒ DF – AB
= (151.5 – 1.5) m = 150 m ......[∵ AB = GF]
Now in ΔBGD,
BG2 + GD2 = BD2 ......(By Pythagoras Theorem)
⇒ x2 + (150)2 = (250)2
⇒ x2 + 22500 = 62500
⇒ x2 = 62500 – 22500
⇒ x2 = 40000
⇒ x2 = 40000
Let initially the length of the string be y m
∴ In ΔBGD
BG2 + GD2 = BD2
⇒ x2 + (150)2 = y2
Differentiating both sides w.r.t., t, we get
⇒ `2x * "dx"/"dt" + 0 = 2y * "dy"/"dt"` ......`[because "dx"/"dt" = 10 "m"/"s"]`
⇒ 2 × 200 × 10 = 2 × 250 × `"dy"/"dt"`
∴ `"dy"/"dt" = (2 xx 200 xx 10)/(2 xx 250)` = 8 m/s
Hence, the rate of change of the length of the string is 8 m/s.
APPEARS IN
RELATED QUESTIONS
If y = f (u) is a differential function of u and u = g(x) is a differential function of x, then prove that y = f [g(x)] is a differential function of x and `dy/dx=dy/(du) xx (du)/dx`
The radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?
The radius of an air bubble is increasing at the rate `1/2` cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
The total cost C(x) in rupees associated with the production of x units of an item is given by C(x) = 0.007x3 – 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced
The rate of change of the area of a circle with respect to its radius r at r = 6 cm is ______.
The total cost C(x) associated with the production of x units of an item is given by C(x) = 0.005x3 – 0.02x2 + 30x + 5000. Find the marginal cost when 3 units are produced, whereby marginal cost we mean the instantaneous rate of change of total cost at any level of output.
Find the rate of change of the volume of a sphere with respect to its surface area when the radius is 2 cm ?
The radius of a circle is increasing at the rate of 0.7 cm/sec. What is the rate of increase of its circumference?
A balloon which always remains spherical, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon is increasing when the radius is 15 cm.
A man 2 metres high walks at a uniform speed of 5 km/hr away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases.
A balloon in the form of a right circular cone surmounted by a hemisphere, having a diameter equal to the height of the cone, is being inflated. How fast is its volume changing with respect to its total height h, when h = 9 cm.
The radius of a cylinder is increasing at the rate 2 cm/sec. and its altitude is decreasing at the rate of 3 cm/sec. Find the rate of change of volume when radius is 3 cm and altitude 5 cm.
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of the perimeter.
Find the surface area of a sphere when its volume is changing at the same rate as its radius ?
If the rate of change of volume of a sphere is equal to the rate of change of its radius, find the radius of the sphere ?
If \[V = \frac{4}{3}\pi r^3\] , at what rate in cubic units is V increasing when r = 10 and \[\frac{dr}{dt} = 0 . 01\] ? _________________
Side of an equilateral triangle expands at the rate of 2 cm/sec. The rate of increase of its area when each side is 10 cm is
The coordinates of the point on the ellipse 16x2 + 9y2 = 400 where the ordinate decreases at the same rate at which the abscissa increases, are
The radius of the base of a cone is increasing at the rate of 3 cm/minute and the altitude is decreasing at the rate of 4 cm/minute. The rate of change of lateral surface when the radius = 7 cm and altitude 24 cm is
The radius of a circular plate is increasing at the rate of 0.01 cm/sec. The rate of increase of its area when the radius is 12 cm, is
A man 2 metres tall walks away from a lamp post 5 metres height at the rate of 4.8 km/hr. The rate of increase of the length of his shadow is
Evaluate: `int (x(1+x^2))/(1+x^4)dx`
A man, 2m tall, walks at the rate of `1 2/3` m/s towards a street light which is `5 1/3`m above the ground. At what rate is the tip of his shadow moving? At what rate is the length of the shadow changing when he is `3 1/3`m from the base of the light?
The volume of a cube increases at a constant rate. Prove that the increase in its surface area varies inversely as the length of the side
A particle is moving along the curve x = at2 + bt + c. If ac = b2, then particle would be moving with uniform ____________.
If the rate of change of the area of the circle is equal to the rate of change of its diameter then its radius is equal to ____________.
The radius of a circle is increasing uniformly at the rate of 3 cm per second. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
A kite is being pulled down by a string that goes through a ring on the ground 8 meters away from the person pulling it. If the string is pulled in at 1 meter per second, how fast is the kite coming down when it is 15 meters high?
