Advertisements
Advertisements
प्रश्न
A kite is being pulled down by a string that goes through a ring on the ground 8 meters away from the person pulling it. If the string is pulled in at 1 meter per second, how fast is the kite coming down when it is 15 meters high?
उत्तर
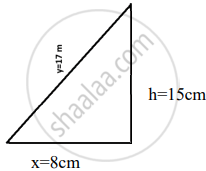
x2 + h2 = y2
`\implies` x2 + 225 = y2
Given, `dy/dx` = 1 m/sec
Differentiating w.r.t ‘t’
`2xdx/dt = 2ydy/dt`
`8 xx dx/dt = 17 xx 1`
APPEARS IN
संबंधित प्रश्न
A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm/s. At the instant when the radius of the circular wave is 8 cm, how fast is the enclosed area increasing?
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.
A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the later is 10 cm.
The radius of an air bubble is increasing at the rate `1/2` cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
The total cost C(x) in rupees associated with the production of x units of an item is given by C(x) = 0.007x3 – 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced
Find the rate of change of the volume of a sphere with respect to its diameter ?
The radius of a spherical soap bubble is increasing at the rate of 0.2 cm/sec. Find the rate of increase of its surface area, when the radius is 7 cm.
A particle moves along the curve y = x3. Find the points on the curve at which the y-coordinate changes three times more rapidly than the x-coordinate.
A man 2 metres high walks at a uniform speed of 6 km/h away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases ?
The volume of metal in a hollow sphere is constant. If the inner radius is increasing at the rate of 1 cm/sec, find the rate of increase of the outer radius when the radii are 4 cm and 8 cm respectively.
Find the point on the curve y2 = 8x for which the abscissa and ordinate change at the same rate ?
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of the perimeter.
If a particle moves in a straight line such that the distance travelled in time t is given by s = t3 − 6t2+ 9t + 8. Find the initial velocity of the particle ?
A cone whose height is always equal to its diameter is increasing in volume at the rate of 40 cm3/sec. At what rate is the radius increasing when its circular base area is 1 m2?
If the rate of change of area of a circle is equal to the rate of change of its diameter, then its radius is equal to
Each side of an equilateral triangle is increasing at the rate of 8 cm/hr. The rate of increase of its area when side is 2 cm, is
A man 2 metres tall walks away from a lamp post 5 metres height at the rate of 4.8 km/hr. The rate of increase of the length of his shadow is
In a sphere the rate of change of volume is
Evaluate: `int (x(1+x^2))/(1+x^4)dx`
The rate of change of volume of a sphere with respect to its surface area, when the radius is 2 cm, is ______.
A man, 2m tall, walks at the rate of `1 2/3` m/s towards a street light which is `5 1/3`m above the ground. At what rate is the tip of his shadow moving? At what rate is the length of the shadow changing when he is `3 1/3`m from the base of the light?
A swimming pool is to be drained for cleaning. If L represents the number of litres of water in the pool t seconds after the pool has been plugged off to drain and L = 200 (10 – t)2. How fast is the water running out at the end of 5 seconds? What is the average rate at which the water flows out during the first 5 seconds?
The volume of a cube increases at a constant rate. Prove that the increase in its surface area varies inversely as the length of the side
A cylindrical tank of radius 10 feet is being filled with wheat at the rate of 3/4 cubic feet per minute. The then depth of the wheat is increasing at the rate of
A spherical balloon is filled with 4500π cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of 72π cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases 49 minutes after the leakage began is ______.
The median of an equilateral triangle is increasing at the ratio of `2sqrt(3)` cm/s. Find the rate at which its side is increasing.
